3.13. Code Tuning and Empirical Analysis¶
3.13.1. Code Tuning and Empirical Analysis¶
In practice, there is not such a big difference in running time between an algorithm with growth rate \(\Theta(n)\) and another with growth rate \(\Theta(n \log n)\). There is, however, an enormous difference in running time between algorithms with growth rates of \(\Theta(n \log n)\) and \(\Theta(n^2)\). As you shall see during the course of your study of common data structures and algorithms, there are many problems whose obvious solution requires \(\Theta(n^2)\) time, but that also have a solution requiring \(\Theta(n \log n)\) time. Examples include sorting and searching, two of the most important computer problems.
While not nearly so important as changing an algorithm to reduce its growth rate, “code tuning” can also lead to dramatic improvements in running time. Code tuning is the art of hand-optimizing a program to run faster or require less storage. For many programs, code tuning can reduce running time or cut the storage requirements by a factor of two or more. Even speedups by a factor of five to ten are not uncommon. Occasionally, you can get an even bigger speedup by converting from a symbolic representation of the data to a numeric coding scheme on which you can do direct computation.
Todo
- type: text
Give an example of this type of representational change.
Here are some suggestions for ways to speed up your programs by code tuning. The most important thing to realize is that most statements in a program do not have much effect on the running time of that program. There are normally just a few key subroutines, possibly even key lines of code within the key subroutines, that account for most of the running time. There is little point to cutting in half the running time of a subroutine that accounts for only 1% of the total running time. Focus your attention on those parts of the program that have the most impact.
When tuning code, it is important to gather good timing statistics. Many compilers and operating systems include profilers and other special tools to help gather information on both time and space use. These are invaluable when trying to make a program more efficient, because they can tell you where to invest your effort.
A lot of code tuning is based on the principle of avoiding work rather than speeding up work. A common situation occurs when we can test for a condition that lets us skip some work. However, such a test is never completely free. Care must be taken that the cost of the test does not exceed the amount of work saved. While one test might be cheaper than the work potentially saved, the test must always be made and the work can be avoided only some fraction of the time.
Example 3.14.1
A common operation in computer graphics applications is to find which among a set of complex objects contains a given point in space. Many useful data structures and algorithms have been developed to deal with variations of this problem. Most such implementations involve the following tuning step. Directly testing whether a given complex object contains the point in question is relatively expensive. Instead, we can screen for whether the point is contained within a bounding box for the object. The bounding box is simply the smallest rectangle (usually defined to have sides perpendicular to the \(x\) and \(y\) axes) that contains the object. If the point is not in the bounding box, then it cannot be in the object. If the point is in the bounding box, only then would we conduct the full comparison of the object versus the point. Note that if the point is outside the bounding box, we saved time because the bounding box test is cheaper than the comparison of the full object versus the point. But if the point is inside the bounding box, then that test is redundant because we still have to compare the point against the object. Typically the amount of work avoided by making this test is greater than the cost of making the test on every object.
Be careful not to use tricks that make the program unreadable. Most code tuning is simply cleaning up a carelessly written program, not taking a clear program and adding tricks. In particular, you should develop an appreciation for the capabilities of modern compilers to make extremely good optimizations of expressions. “Optimization of expressions” here means a rearrangement of arithmetic or logical expressions to run more efficiently. Be careful not to damage the compiler’s ability to do such optimizations for you in an effort to optimize the expression yourself. Always check that your “optimizations” really do improve the program by running the program before and after the change on a suitable benchmark set of input. Many times I have been wrong about the positive effects of code tuning in my own programs. Most often I am wrong when I try to optimize an expression. It is hard to do better than the compiler.
The greatest time and space improvements come from a better data structure or algorithm. The most important rule of code tuning is:
First tune the algorithm, then tune the code.
3.13.1.1. Empirical Analysis¶
Asymptotic algorithm analysis is an analytic tool, whereby we model the key aspects of an algorithm to determine the growth rate of the algorithm as the input size grows. It has proved hugely practical, guiding developers to use more efficient algorithms. But it is really an estimation technique, and it has its limitations. These include the effects at small problem size, determining the finer distinctions between algorithms with the same growth rate, and the inherent difficulty of doing mathematical modeling for more complex problems.
An alternative to analytical approaches are empirical ones. The most obvious empirical approach is simply to run two competitors and see which performs better. In this way we might overcome the deficiencies of analytical approaches.
Be warned that comparative timing of programs is a difficult business, often subject to experimental errors arising from uncontrolled factors (system load, the language or compiler used, etc.). The most important concern is that you might be biased in favor of one of the programs. If you are biased, this is certain to be reflected in the timings. One look at competing software or hardware vendors’ advertisements should convince you of this. The most common pitfall when writing two programs to compare their performance is that one receives more code-tuning effort than the other, since code tuning can often reduce running time by a factor of five to ten. If the running times for two programs differ by a constant factor regardless of input size (i.e., their growth rates are the same), then differences in code tuning might account for any difference in running time. Be suspicious of empirical comparisons in this situation.
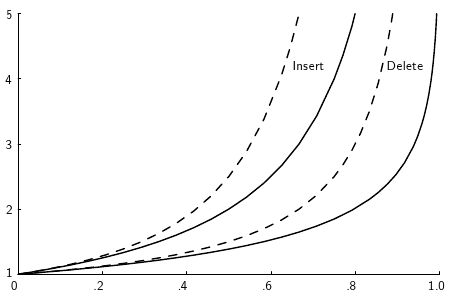
Another approach to analytical analysis is simulation. The idea of simulation is to model the problem with a computer program and then run it to get a result. In the context of algorithm analysis, simulation is distinct from empirical comparison of two competitors because the purpose of the simulation is to perform analysis that might otherwise be too difficult. A good example of this appears in the following figure.
This figure shows the cost for inserting or deleting a record from a hash table under two different assumptions for the policy used to find a free slot in the table. The \(y\) axes is the cost in number of hash table slots evaluated, and the \(x\) axes is the percentage of slots in the table that are full. The mathematical equations for these curves can be determined, but this is not so easy. A reasonable alternative is to write simple variations on hashing. By timing the cost of the program for various loading conditions, it is not difficult to construct a plot similar to this one. The purpose of this analysis was not to determine which approach to hashing is most efficient, so we are not doing empirical comparison of hashing alternatives. Instead, the purpose was to analyze the proper loading factor that would be used in an efficient hashing system to balance time cost versus hash table size (space cost).