1.7 Abstract data types
Earlier, we introduced the term data type, which refers to a type along with a collection of operations for manipulating values of that type. For instance, integers form a data type, and addition is an operation that can be performed on them. These are known as concrete data types, meaning they consist of actual values and a specific implementation. In contrast, an abstract data type (ADT) does not specify concrete values or implementations. Instead, it defines a data type purely in terms of a set of operations and the expected behaviour of those operations, as determined by their inputs and outputs. An ADT does not dictate how the operations should be implemented, and multiple implementations are often possible. These implementation details are hidden from the user—a concept known as encapsulation. The set of operations offered by an abstract data type is known as its application programming interface (API).
Using an ADT, we can distinguish between the logical behaviour of a data type and its actual implementation in a concrete program. A classic example is the list abstract data type, which support the following set of operations:
interface List of T:
add(i: Int, x: T) // Adds x at position i; where 0 ≤ i ≤ size.
get(i: Int) -> T // Returns the element at position i; where 0 ≤ i < size.
set(i: Int, x: T) // Replaces the value at position i with x; where 0 ≤ i < size.
remove(i: Int) // Removes the element at position i; where 0 ≤ i < size.A list can be implemented using either an array or a linked list. Users of a list do not need to know which implementation is used in order to make use of its functionality. The actual implementations of an ADT rely on specific data structures to realise the desired behaviour of the operations – for example, calculating the size of a list.
Although different implementations of an abstract data type offer the same set of operations, the choice of data structure can significantly impact the efficiency of those operations. Often, there are trade-offs involved: optimising one operation may come at the cost of another. For example, an array-based list allows fast access to elements at specific indices, while a linked-list implementation excels at inserting elements at the front. Furthermore, different applications may prioritise different operations. One program might frequently perform operation A, while another relies more heavily on operation B. In such cases, it is often not possible to implement all operations efficiently, so multiple implementations of the same ADT are needed. Additionally, one implementation may be more efficient for small datasets (thousands of elements), whereas another may scale better for large datasets (millions of elements). The most suitable data structure depends on the specific use case, and making informed and well-reasoned choices is one of the central goals of this book.
Example: Collection of records
A database is a structured collection of data that can be easily accessed, managed, and updated. Each item in a database is typically called a record, which consists of multiple fields containing information—such as a name, an ID number, or an address. Efficiently organising, storing, and searching these records is a key challenge in database design.
Two popular implementations for managing large disk-based database applications are hashing and the B-tree. Both support efficient insertion and deletion of records, as well as exact-match queries. However, they differ in the types of queries they handle best. Hashing is particularly efficient for exact-match queries, where you are looking for a record with a specific key. On the other hand, B-trees are better suited for range queries, where you want to retrieve all records with keys within a certain interval. In such cases, hashing becomes inefficient.
Therefore, if a database application only requires exact-match queries, hashing is typically the better choice. But if the application needs to support range queries—such as finding all records with values between X and Y—the B-tree is preferred. Despite their performance differences, both data structures address the same core problem: how to efficiently update and search a large collection of records.
The concept of an ADT can help us to focus on key issues even in non-computing applications.
Example: Cars
When operating a car, the primary activities are steering, accelerating, and braking. On nearly all passenger cars, you steer by turning the steering wheel, accelerate by pushing the gas pedal, and brake by pushing the brake pedal. This design for cars can be viewed as an ADT with operations “steer”, “accelerate”, and “brake”. Two cars might implement these operations in radically different ways, say with different types of engine, or front- versus rear-wheel drive. Yet, most drivers can operate many different cars because the ADT presents a uniform method of operation that does not require the driver to understand the specifics of any particular engine or drive design. These differences are deliberately hidden.
The concept of an ADT is one instance of an important principle that must be understood by any successful computer scientist: managing complexity through abstraction. A central theme of computer science is complexity and techniques for handling it. Humans deal with complexity by assigning a label to an assembly of objects or concepts and then manipulating the label in place of the assembly. Cognitive psychologists call such a label a metaphor. A particular label might be related to other pieces of information or other labels. This collection can in turn be given a label, forming a hierarchy of concepts and labels. This hierarchy of labels allows us to focus on important issues while ignoring unnecessary details.
Example: Computers, hard drives, and CPUs
We apply the label “hard drive” to a collection of hardware that manipulates data on a particular type of storage device, and we apply the label “CPU” to the hardware that controls execution of computer instructions. These and other labels are gathered together under the label “computer”. Because even the smallest home computers today have millions of components, some form of abstraction is necessary to comprehend how a computer operates.
Consider how you might go about the process of designing a complex computer program that implements and manipulates an ADT. The ADT is implemented in one part of the program by a particular data structure. While designing those parts of the program that use the ADT, you can think in terms of operations on the data type without concern for the data structure’s implementation. Without this ability to simplify your thinking about a complex program, you would have no hope of understanding or implementing it.
Most of the abstract data types we introduce in this book are collections, that is, structures that store elements of an arbitrary type. The earlier example of a list illustrates this: a list is a collection that holds elements, which can be of any type.
We group these collection-based ADTs into two main categories:
- Linear collections
- Sets and maps
In addition to these, we also introduce graphs, along with their commonly used implementations.
The rest of this gives a high-level overview of the ADTs covered throughout the course. Figure 1.1 summarises these ADTs and highlights how they relate to one another. Each ADT will be discussed in more detail later in the book, including their operations and the data structures used to implement them.
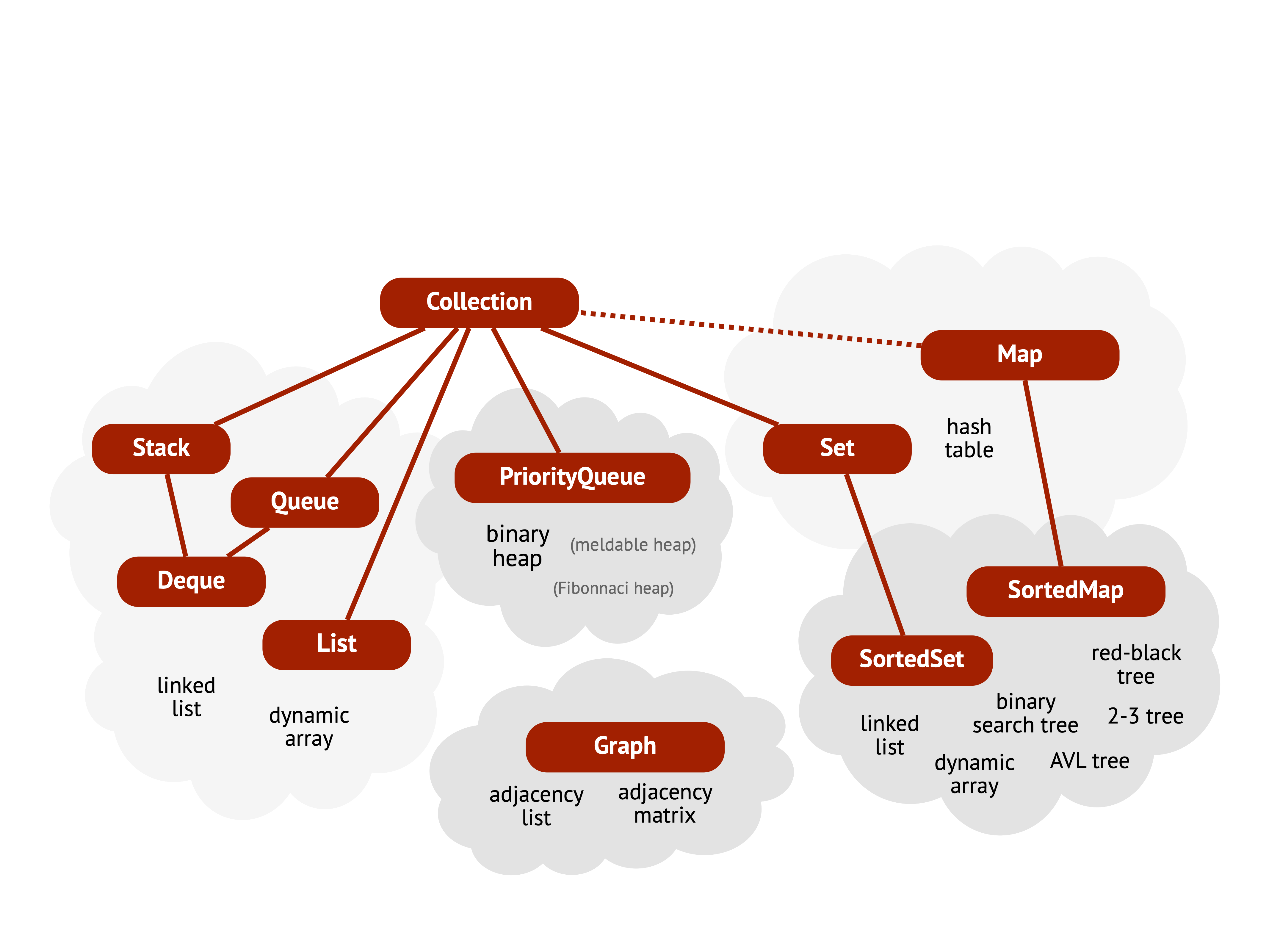
1.7.1 Linear collections
Linear collections are a category of abstract data types in which the order of the elements matters. This means that each element has a specific position in the sequence, and operations on the ADT are sensitive to this order. Insertion, removal, and retrieval operations often depend on the position within the sequence.
The ordered sequence ADTs found in this book are:
Stacks: sequences with a Last-In-First-Out (LIFO) ordering
Queues: sequences with a First-In-First-Out (FIFO) ordering
Double-ended queues (deques): allow insertion and removal at both ends
Priority queues: return elements based on priority rather than insertion order
General lists: support adding, removing, and accessing elements
Ordered sequences are used in many applications and algorithms where the order of operations or items is important. For example, maintaining a task list, simulating a line of customers, or a editor’s undo/redo history.
1.7.2 Sets and maps
Many programming tasks involve retrieving specific information from a large dataset. For example, given a collection of people, how do we efficiently find the person with a specific personnummer? Two key abstract data types are commonly used to solve such information retrieval problems:
Sets: represent unordered collections of distinct items. They support operations to add and remove elements, and to check whether a particular element is present. Duplicate elements are not allowed.
Maps (also called dictionaries): represent collections of key-value pairs, where each key maps to a corresponding value. Operations include adding or removing key-value pairs, checking if a key is present, and retrieving the value associated with a given key. Like sets, maps do not allow duplicate keys.
Most implementations of both sets and maps are designed to support fast insertion, deletion, and lookup operations, making them ideal for managing collections where quick access to data is important.
1.7.3 Graphs
Another well-known abstract data type is the graph. Graphs are used to model relationships between elements, where each element is called a node or vertex. A relation between two nodes is represented by an edge, which may carry additional information to describe the nature or strength of the relationship—such as distance, cost, or capacity.
Graphs appear in many real-world scenarios, often in surprising ways. A classic example is a map, where cities are represented as nodes and roads (with distances) as edges. Graph algorithms can then be used to solve problems such as finding the shortest route between two cities. Another, less obvious example is the structure of Java programs: the dependencies between Java classes can be represented as a graph. This representation helps us determine the correct order to compile classes based on their dependencies.
Graphs are a fundamental concept in computer science, and we dedicate an entire chapter to them in this book. Chapter 13 explores how graphs can be represented and how we can traverse and manipulate them using various algorithms.