DSABook – AVL trees

11.3 AVL trees

The AVL tree is a BST with the following additional property:

For every node, the heights of its subtrees differ by at most 1.

As long as the tree maintains this property, if the tree contains $n$ nodes, then it has a depth of at most $O(\log n)$ . As a result, search for any node will cost $O(\log n)$ , and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost $O(\log n)$ , even in the worst case.

The key to making the AVL tree work is to alter the insert and delete routines so as to maintain the balance property. Of course, to be practical, we must be able to implement the revised update routines in $O(\log n)$ time. To maintain the balance property, we are going to use what are called rotations.

11.3.1 Rotations

Rotation is an operation that takes a node in the tree and moves it one level higher. Figure 11.3 illustrates rotation. Here, $P$ and $S$ are nodes, while $A$ , $B$ and $C$ represent subtrees.

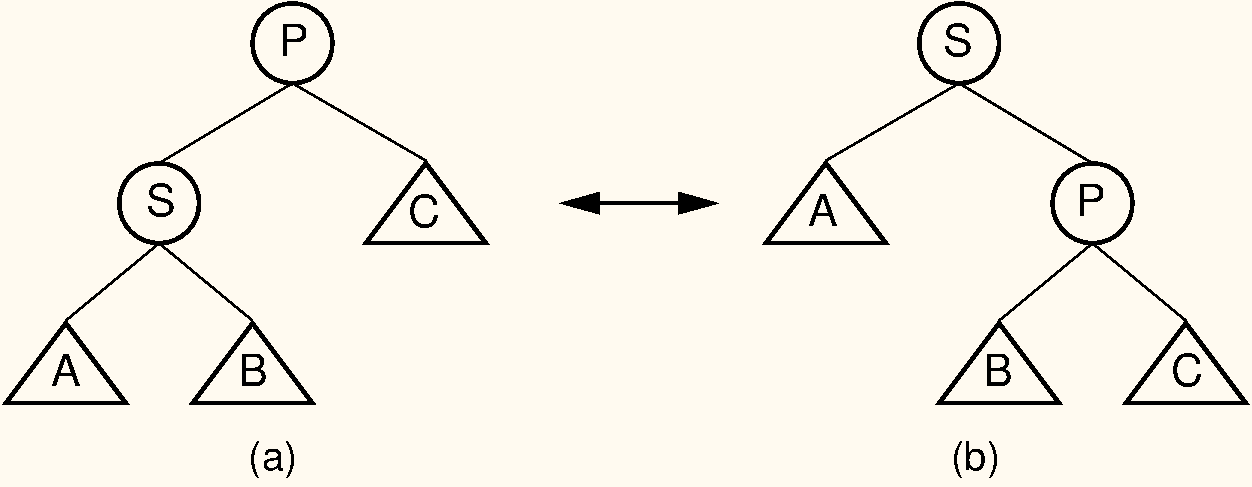
Figure 11.3: Rotation. In a rotation, node S is promoted to the root, rotating with node P. Because the value of S is less than the value of P, P must become S ’s right child. The positions of subtrees A, B, and C are altered as appropriate to maintain the BST property, but the contents of these subtrees remains unchanged. (a) The original tree with P as the parent. (b) The tree after a rotation takes place. Going from (a) to (b) is called a right rotation. We can also go from (b) to (a) promoting node P to the root – this is called a left rotation. In general, a right rotation makes the tree more right-leaning, and a left rotation makes it more left-leaning. — Figure 11.3: Rotation. In a rotation, node $S$ is promoted to the root, rotating with node $P$ . Because the value of $S$ is less than the value of $P$ , $P$ must become $S$ ’s right child. The positions of subtrees $A$ , $B$ , and $C$ are altered as appropriate to maintain the BST property, but the contents of these subtrees remains unchanged. (a) The original tree with $P$ as the parent. (b) The tree after a rotation takes place. Going from (a) to (b) is called a *right rotation*. We can also go from (b) to (a) promoting node $P$ to the root – this is called a *left rotation*. In general, a right rotation makes the tree more right-leaning, and a left rotation makes it more left-leaning.

In figure (a), node $S$ is the left child of the root. A right rotation transforms it into the tree shown in figure (b), where node $S$ has become the root. Note that, because the value of $S$ is less than the value of $P$ , $P$ must become $S$ ’s right child. Right rotation means transforming a tree from having the shape in (a) to having the shape in (b).

A left rotation is the opposite process: starting from the tree in (b), transforming it to the tree in (a), by lifting node $P$ up. Notice that a right rotation tends to make the tree more right-leaning, while a left rotation tends to make it more left-leaning.

11.3.2 AVL tree insertion

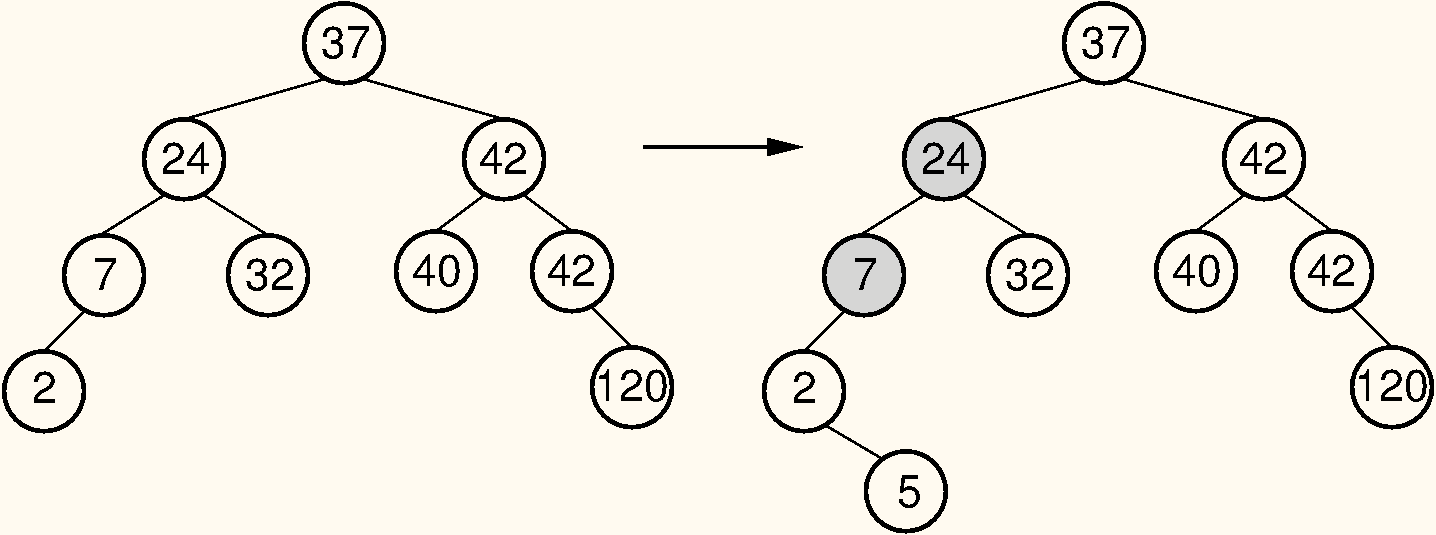
Figure 11.4: An insertion that violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced.

Consider what happens when we insert a node with key value 5, as shown in Figure 11.4. The tree on the left meets the AVL tree balance requirements. After the insertion, two nodes no longer meet the requirements. Because the original tree met the balance requirement, nodes in the new tree can only be unbalanced by a difference of at most 2 in the subtrees. For the bottommost unbalanced node, call it $S$ , there are 4 cases:

The extra node is in the left child of the left child of $S$ .
The extra node is in the right child of the left child of $S$ .
The extra node is in the left child of the right child of $S$ .
The extra node is in the right child of the right child of $S$ .

Cases 1 and 4 are symmetric, as are cases 2 and 3. Note also that the unbalanced nodes must be on the path from the root to the newly inserted node.

Our problem now is how to balance the tree in $O(\log n)$ time. It turns out that we can do this using a series of rotations. Cases 1 and 4 can be fixed using a single rotation, as shown in Figure 11.5. Cases 2 and 3 can be fixed using a double rotation, as shown in Figure 11.6.

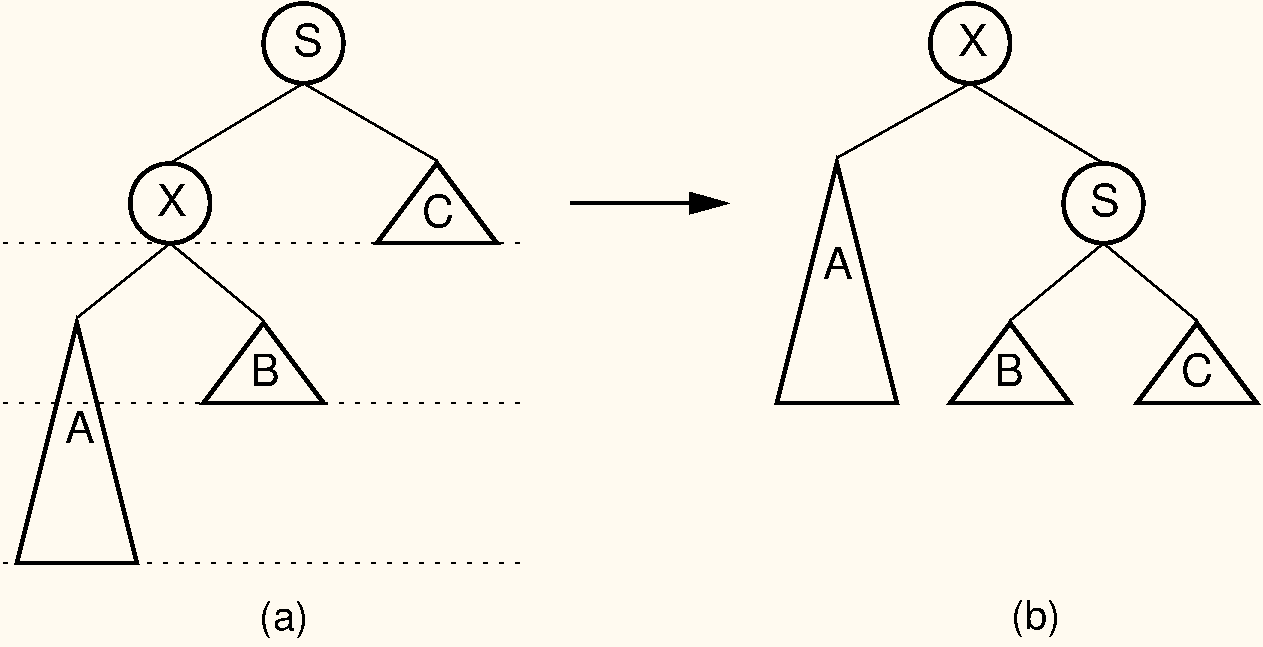
Figure 11.5: A single rotation in an AVL tree. This operation occurs when the excess node (in subtree A) is in the left child of the left child of the unbalanced node labeled S. By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the right child of the right child of the unbalanced node is handled in the same way. — Figure 11.5: A single rotation in an AVL tree. This operation occurs when the excess node (in subtree $A$ ) is in the left child of the left child of the unbalanced node labeled $S$ . By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the right child of the right child of the unbalanced node is handled in the same way.

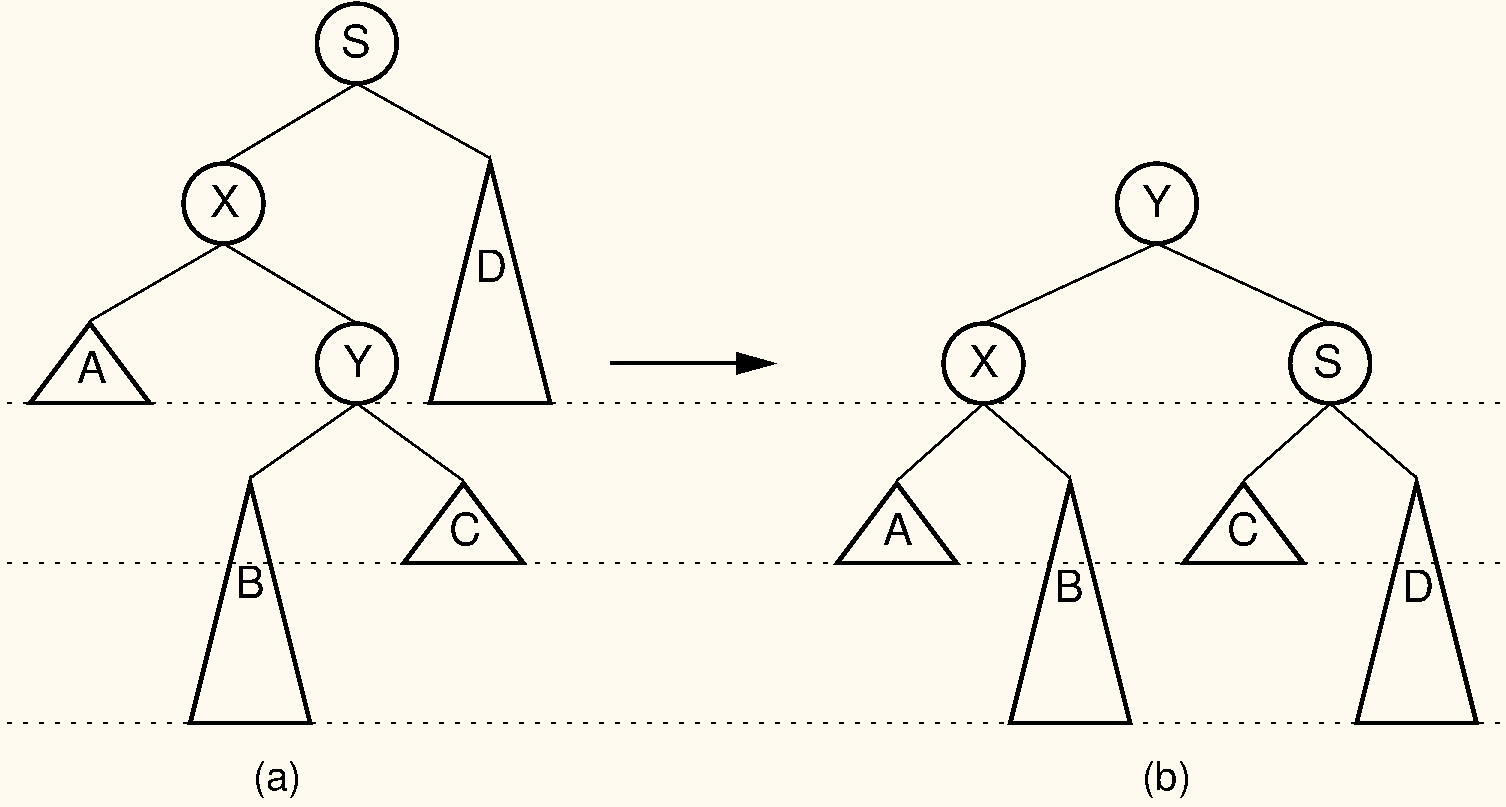
Figure 11.6: A double rotation in an AVL tree. This operation occurs when the excess node (in subtree B) is in the right child of the left child of the unbalanced node labeled S. By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the left child of the right child of S is handled in the same way. — Figure 11.6: A double rotation in an AVL tree. This operation occurs when the excess node (in subtree $B$ ) is in the right child of the left child of the unbalanced node labeled $S$ . By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the left child of the right child of $S$ is handled in the same way.

AVL tree insertion and deletion are easiest to implement as recursive functions. They are very similar to the normal BST insertion and deletion, but as the recursion unwinds up the tree, we perform the appropriate rotation on any node that is found to be unbalanced.

Example: AVL insertion

In Figure 11.4 (b), the bottom-most unbalanced node has value 7. The excess node (with value 5) is in the right subtree of the left child of 7, so we have an example of Case 2. This requires a double rotation to fix. After the rotation, 5 becomes the left child of 24, 2 becomes the left child of 5, and 7 becomes the right child of 5.

To try out AVL insertion yourself and see how it works, see the AVL tree visualisation here: https://chalmersgu-data-structure-courses.github.io/dsvis/collections.html

Here is an implementation of AVL trees:

datatype AVLNode of K, V extends BSTNode:
    ...key, value, left, right  // All properties of the BSTNode
    height: Int = 1             // The height of this subtree.


datatype AVLMap extends BSTMap:
    ...root, size   // All properties of the BSTMap
    ...get(key)     // Inherited from BSTMap

    put(key, value):
        // Add a key-value pair, or update the value associated with an existing key.
        // This is the same as BSTMap.put, except that it rebalances the node afterwards.
        root = putHelper(root, key, value)

    putHelper(node, key, value):
        // Recursive helper method for 'put', returns the updated node.
        if node is null:
            size = size + 1
            return new AVLNode(key, value)
        else if key < node.key:
            node.left = putHelper(node.left, key, value)
            updateHeight(node)
        else if key > node.key:
            node.right = putHelper(node.right, key, value)
            updateHeight(node)
        else: // key == node.key
            node.value = value
        return rebalance(node)

    remove(key):
        // Delete a key and its associated value.
        // This is the same as BSTMap.remove, except that it rebalances the node afterwards.
        root = removeHelper(root, key)

    removeHelper(node, key):
        // Helper method for 'remove', returns the updated node.
        if node is null:
            return null
        else if key < node.key:
            node.left = removeHelper(node.left, key)
            updateHeight(node)
            return rebalance(node)
        else if key > node.key:
            node.right = removeHelper(node.right, key)
            updateHeight(node)
            return rebalance(node)
        else: // key == node.key
            if node.left is null:
                size = size - 1
                return node.right
            else if node.right is null:
                size = size - 1
                return node.left
            else:
                predecessor = largestNode(node.left)
                old_value = node.value
                node.key = predecessor.key
                node.value = predecessor.value
                node.left = removeHelper(node.left, predecessor.key)
                updateHeight(node)
                return rebalance(node)

Here are some helper functions:

getHeight(node):
    // Return the height of a tree node, also works if the node is null.
    if node is null:
        return 0
    else:
        return node.height

updateHeight(node):
    // Recompute the value of the height of a tree node.
    // Must be called every time the height could change.
    node.height = 1 + max(getHeight(node.left), getHeight(node.right))

heightDiff(node):
    // Return the height difference of a node: left height - right height.
    return getHeight(node.left) - getHeight(node.right)

largestNode(node):
    // Find the descendant node having the largest key.
    while node.right is not null:
        node = node.right
    return node

rebalance(node):
    if node is null:
        return null
    diff = heightDiff(node)
    if diff > 1:  // Left-leaning
        leftDiff = heightDiff(node.left)
        if leftDiff == -1:  // Left-right: convert to left-left
            node.left = rotateLeft(node.left)
            updateHeight(node)
        return rotateRight(node)
    else if diff < -1:  // Right-leaning
        rightDiff = heightDiff(node.right)
        if rightDiff == 1:  // Right-left: convert to right-right
            node.right = rotateRight(node.right)
            updateHeight(node)
        return rotateLeft(node)
    else:
        return node

rotateLeft(x):
    // Left rotation.
    ("""      x                 y
                / \               / \
            A   y     ===>    x   C
                / \           / \
                B   C         A   B         """)
    // Variables are named according to the picture above.
    y = x.right
    B = y.left
    x.right = B
    y.left = x
    return y

rotateRight(x):
    // Right rotation.
    ("""       x              y
                / \            / \
                y   C   ===>   A   x
            / \                / \
            A   B              B   C       """)
    // Variables are named according to the picture above.
    y = x.left
    B = y.right
    x.left = B
    y.right = x
    return y