As an example, here is a recursive implementation for the factorial function.

// Recursively compute and return n-factoral (n!)
function factorialRecursive(n):
    if n <= 1:
        // Base case: return base solution
        return 1
    else:
        // Recursive call for n > 1
        return n * factorialRecursive(n-1)

Here is an illustration for how the internal processing works.

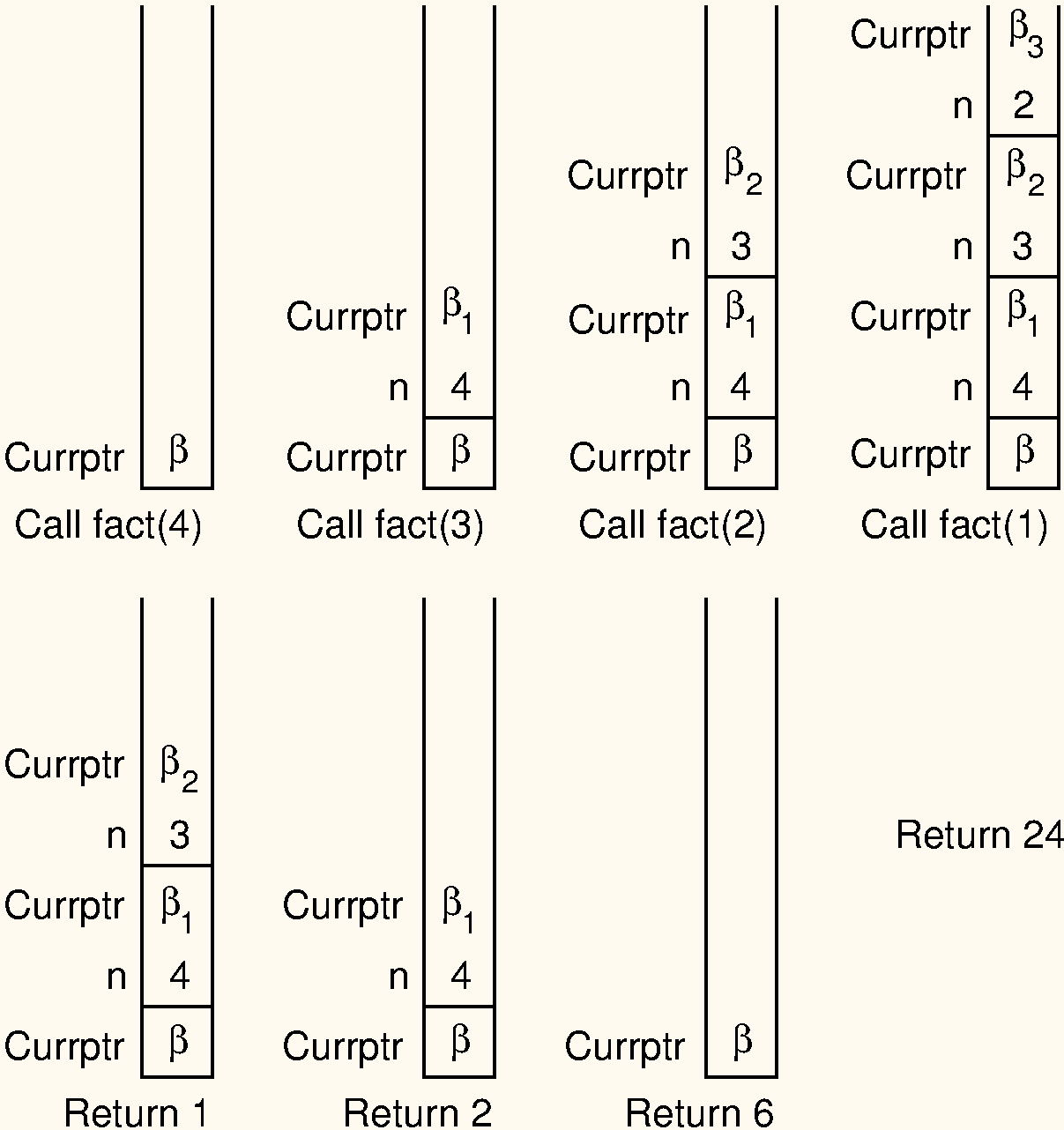
$\beta$ values indicate the address of the program instruction to return to after completing the current function call. On each recursive function call to fact, both the return address and the current value of n must be saved. Each return from fact pops the top activation record off the stack.

Consider what happens when we call fact with the value 4. We use $\beta$ to indicate the address of the program instruction where the call to fact is made. Thus, the stack must first store the address $\beta$, and the value 4 is passed to fact. Next, a recursive call to fact is made, this time with value 3. We will name the program address from which the call is made $\beta_1$. The address $\beta_1$, along with the current value for $n$ (which is 4), is saved on the stack. Function fact is invoked with input parameter 3.

In similar manner, another recursive call is made with input parameter 2, requiring that the address from which the call is made (say $\beta_2$) and the current value for $n$ (which is 3) are stored on the stack. A final recursive call with input parameter 1 is made, requiring that the stack store the calling address (say $\beta_3$) and current value (which is 2).

At this point, we have reached the base case for fact, and so the recursion begins to unwind. Each return from fact involves popping the stored value for $n$ from the stack, along with the return address from the function call. The return value for fact is multiplied by the restored value for $n$, and the result is returned.

Because an activation record must be created and placed onto the stack for each subroutine call, making subroutine calls is a relatively expensive operation. While recursion is often used to make implementation easy and clear, sometimes you might want to eliminate the overhead imposed by the recursive function calls. In some cases, such as the factorial function above, recursion can easily be replaced by iteration.

function factorialStack(n):
    S = new Stack()
    while n > 1:
        S.push(n)
        n = n - 1
    result = 1
    while S.size > 0:
        result = result * S.pop()
    return result

An iterative form of the factorial function is both simpler and faster than the version shown in the example. But it is not always possible to replace recursion with iteration. Recursion, or some imitation of it, is necessary when implementing algorithms that require multiple branching such as in the Towers of Hanoi algorithm, or when traversing a binary tree (Section 8.4). The Mergesort and Quicksort sorting algorithms also require recursion.

Fortunately, it is always possible to imitate recursion with a stack. Recursive algorithms lend themselves to efficient implementation with a stack when the amount of information needed to describe a sub-problem is small. For example, Quicksort can effectively use a stack to replace its recursion since only bounds information for the subarray to be processed needs to be saved.

Let us now turn to a non-recursive version of the Towers of Hanoi function, which cannot be done iteratively.

// Compute the moves to solve a Tower of Hanoi puzzle.
// Function 'move' does (or prints) the actual move of a disk from one pole to another.
function towersRecursive(n, start, goal, temp):
    if n == 0:                               // Base case
        return
    towersRecursive(n-1, start, temp, goal)  // Recursive call: n-1 rings
    move(start, goal)                        // Move bottom disk to goal
    towersRecursive(n-1, temp, goal, start)  // Recursive call: n-1 rings

datatype Task:
    oper: MOVE or TOH
    n: Int
    start, temp, goal: Pole

function towersStack(n, start, goal, temp):
    S = new LinkedStack()
    S.push(new Task(TOH, n, start, goal, temp))
    while S.size > 0:
        it = S.pop()          // Get next task
        if it.oper == MOVE:   // Do a move
            move(it.start, it.goal)
        else if it.num > 0:   // Imitate TOH recursive solution (in reverse)
            S.push(new Task(TOH, it.num-1, it.temp, it.goal, it.start))
            S.push(new Task(MOVE, 0, it.start, it.goal))
            S.push(new Task(TOH, it.num-1, it.start, it.temp, it.goal))