7.5. The AVL Tree¶
The AVL tree is a BST with the following additional property: For every node, the heights of its left and right subtrees differ by at most 1. As long as the tree maintains this property, if the tree contains \(n\) nodes, then it has a depth of at most \(O(\log n)\). As a result, search for any node will cost \(O(\log n)\), and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost \(O(\log n)\), even in the worst case.
The key to making the AVL tree work is to alter the insert and delete routines so as to maintain the balance property. Of course, to be practical, we must be able to implement the revised update routines in \(\Theta(\log n)\) time. To maintain the balance property, we are going to use what are called rotations.
7.5.1. Rotations¶
Rotation is an operation that takes a node in the tree and moves it one level higher. Figure 7.8.1 illustrates rotation. Here, \(P\) and \(S\) are nodes, while \(A\), \(B\) and \(C\) represent subtrees.
In Figure 7.8.1 (a), node \(S\) is the left child of the root. A right rotation transforms it into the tree shown in Figure 7.8.1 (b), where node \(S\) has become the root. Note that, because the value of \(S\) is less than the value of \(P\), \(P\) must become \(S\)’s right child. Right rotation means transforming a tree from having the shape in (a) to having the shape in (b).
A left rotation is the opposite process: starting from the tree in (b), transforming it to the tree in (a), by lifting node \(P\) up. Notice that a right rotation tends to make the tree more right-leaning, while a left rotation tends to make it more left-leaning.
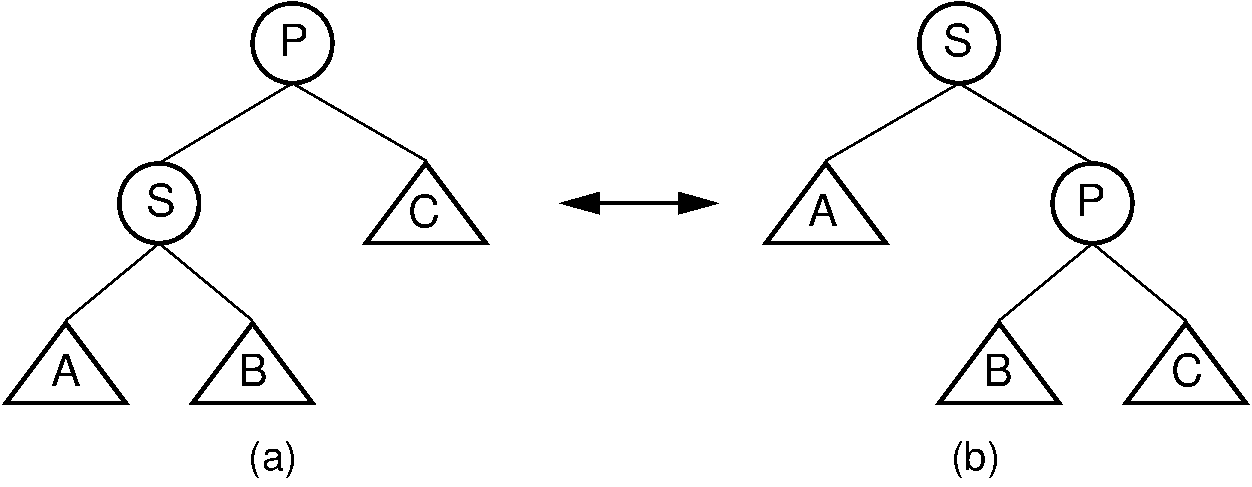
Figure 7.6.1: Rotation. In a rotation, node \(S\) is promoted to the root, rotating with node \(P\). Because the value of \(S\) is less than the value of \(P\), \(P\) must become \(S\) ‘s right child. The positions of subtrees \(A\), \(B\), and \(C\) are altered as appropriate to maintain the BST property, but the contents of these subtrees remains unchanged. (a) The original tree with \(P\) as the parent. (b) The tree after a rotation takes place.¶
Going from (a) to (b) is called a right rotation. We can also go from (b) to (a) promoting node \(P\) to the root – this is called a left rotation. In general, a right rotation makes the tree more right-leaning, and a left rotation makes it more left-leaning.
7.5.2. AVL tree insertion¶
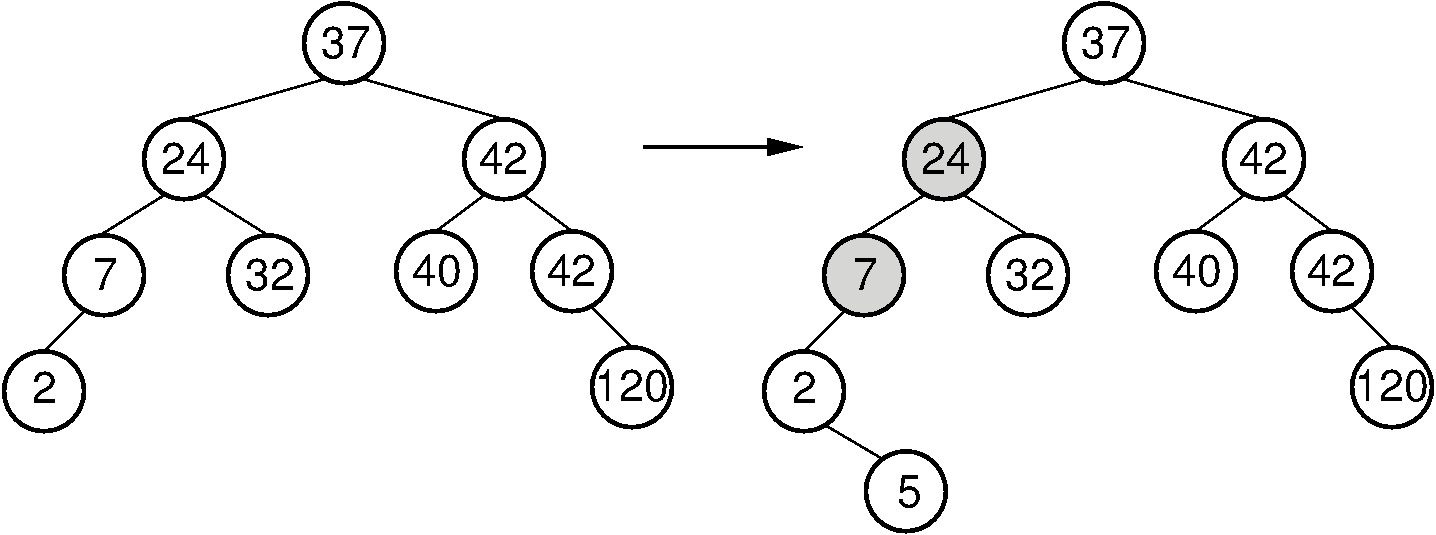
Figure 7.6.2: Example of an insert operation that violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced.¶
Consider what happens when we insert a node with key value 5, as shown in Figure 7.6.2. The tree on the left meets the AVL tree balance requirements. After the insertion, two nodes no longer meet the requirements. Because the original tree met the balance requirement, nodes in the new tree can only be unbalanced by a difference of at most 2 in the subtrees. For the bottommost unbalanced node, call it \(S\), there are 4 cases:
The extra node is in the left child of the left child of \(S\).
The extra node is in the right child of the left child of \(S\).
The extra node is in the left child of the right child of \(S\).
The extra node is in the right child of the right child of \(S\).
Cases 1 and 4 are symmetric, as are cases 2 and 3. Note also that the unbalanced nodes must be on the path from the root to the newly inserted node.
Our problem now is how to balance the tree in \(O(\log n)\) time. It turns out that we can do this using a series of rotations. Cases 1 and 4 can be fixed using a single rotation, as shown in Figure 7.6.3. Cases 2 and 3 can be fixed using a double rotation, as shown in Figure 7.6.4.
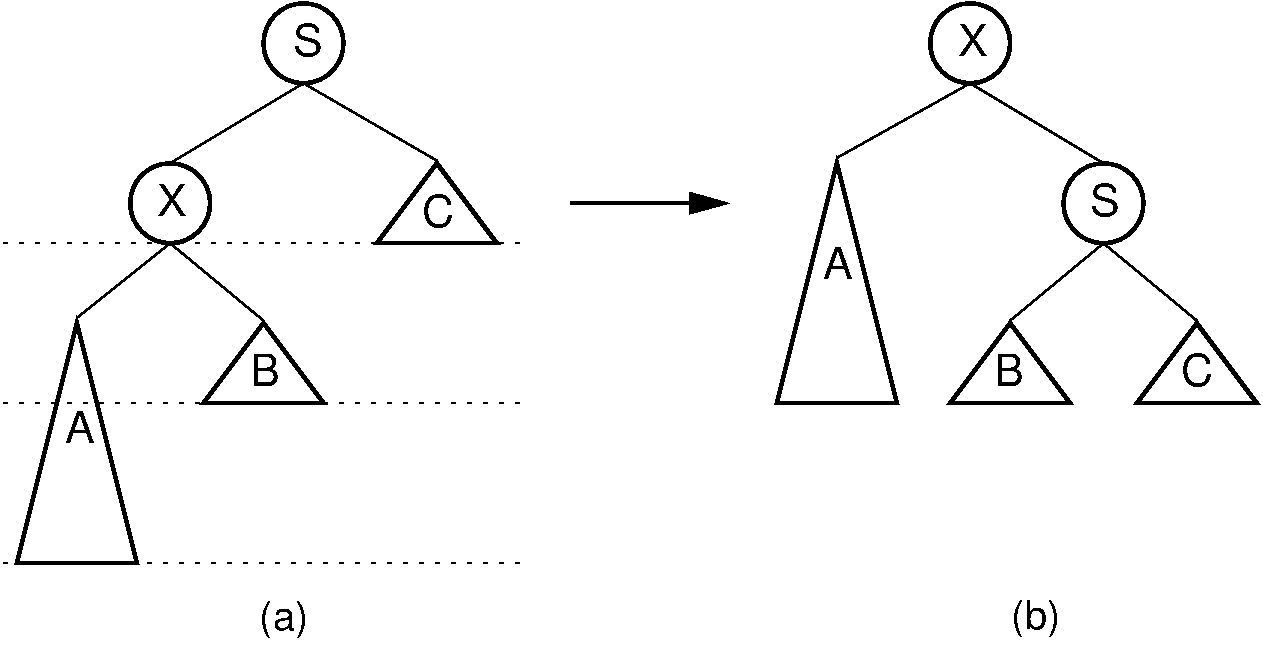
Figure 7.6.3: A single rotation in an AVL tree. This operation occurs when the excess node (in subtree \(A\)) is in the left child of the left child of the unbalanced node labeled \(S\). By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the right child of the right child of the unbalanced node is handled in the same way.¶
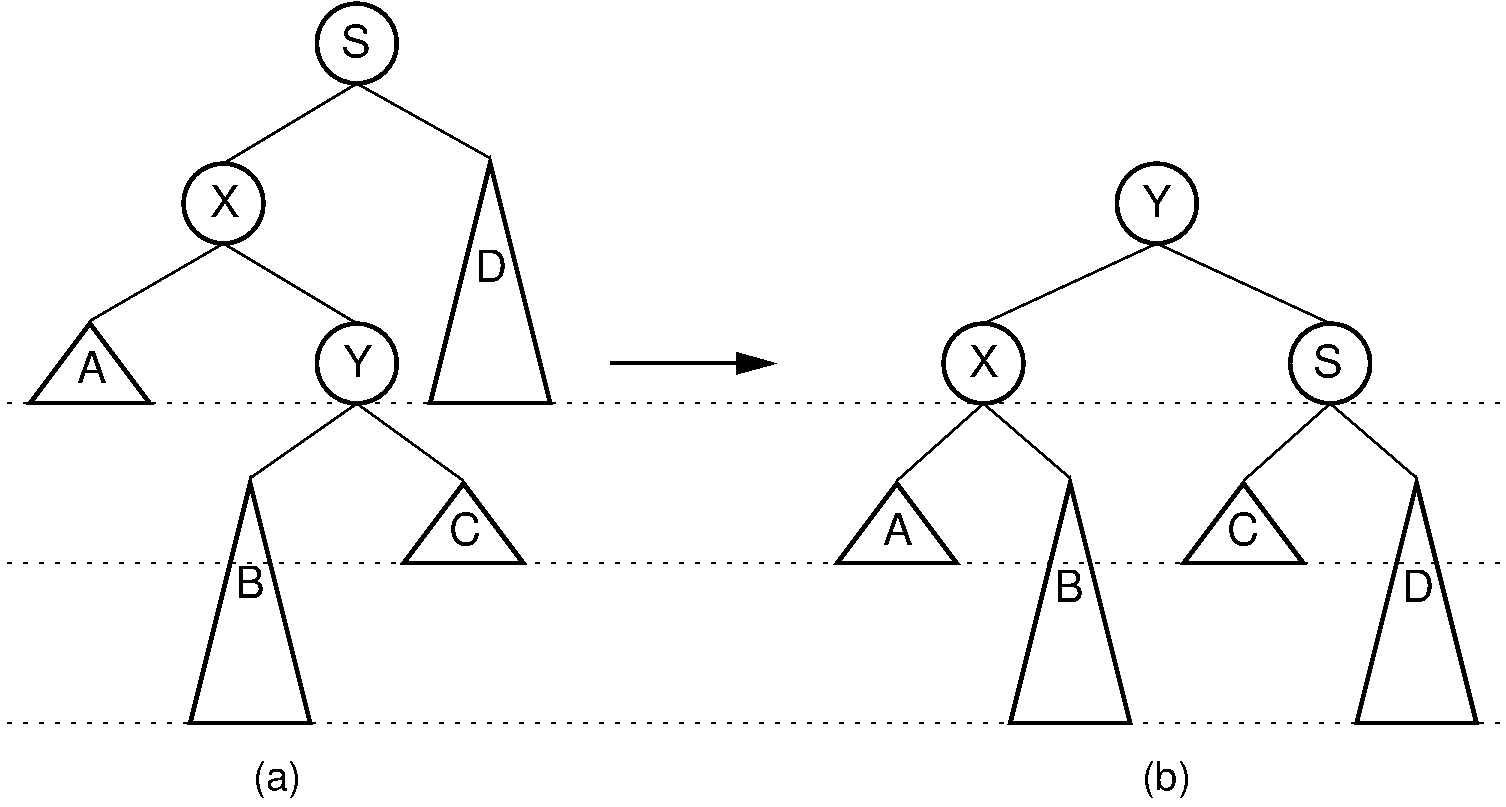
Figure 7.6.4: A double rotation in an AVL tree. This operation occurs when the excess node (in subtree \(B\)) is in the right child of the left child of the unbalanced node labeled \(S\). By rearranging the nodes as shown, we preserve the BST property, as well as re-balance the tree to preserve the AVL tree balance property. The case where the excess node is in the left child of the right child of \(S\) is handled in the same way.¶
The AVL tree insert algorithm begins with a normal BST insert. Then as the recursion unwinds up the tree, we perform the appropriate rotation on any node that is found to be unbalanced. Deletion is similar; however, consideration for unbalanced nodes must begin at the level of the deletemin operation.
Example 7.6.1
In Figure 7.6.2 (b), the bottom-most unbalanced node has value 7. The excess node (with value 5) is in the right subtree of the left child of 7, so we have an example of Case 2. This requires a double rotation to fix. After the rotation, 5 becomes the left child of 24, 2 becomes the left child of 5, and 7 becomes the right child of 5.
To try out AVL insertion yourself and see how it works, see AVL Tree Visualization. You can also find a few more examples under AVL Trees.
Here is an implementation of AVL trees:
// A dictionary implemented using an AVL tree.
public class AVLMap<K extends Comparable<K>, V> implements Map<K, V> {
Node root = null; // The root of the AVL tree.
int treeSize = 0; // The size of the tree.
// A node in an AVL tree.
class Node {
K key;
V value;
Node left;
Node right;
int height;
Node(K key, V value, Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
updateHeight();
}
int getHeight(Node node) {
if (node == null) return 0;
else return node.height;
}
void updateHeight() {
height = 1 + Math.max(getHeight(left), getHeight(right));
}
int heightDiff() {
return getHeight(left) - getHeight(right);
}
}
// Check that the invariant holds.
void checkInvariant() {
int size = checkInvariantHelper(root, null, null);
if (size != treeSize)
throw new AssertionError("wrong tree size");
}
// Recursive helper method for 'check_invariant'.
// Checks that the node is the root of a valid AVL tree, and that
// all keys k satisfy lo < k < hi. The test lo < k is skipped
// if lo is None, and k < hi is skipped if hi is None.
int checkInvariantHelper(Node node, K lo, K hi) {
if (node == null) return 0;
if (lo != null && node.key.compareTo(lo) <= 0)
throw new AssertionError("key too small");
if (hi != null && node.key.compareTo(hi) >= 0)
throw new AssertionError("key too big");
if (node.heightDiff() > 1)
throw new AssertionError("too left-leaning");
if (node.heightDiff() < -1)
throw new AssertionError("too right-leaning");
// Keys in the left subtree should be < node.key
// Keys in the right subtree should be > node.key
return 1 +
checkInvariantHelper(node.left, lo, node.key) +
checkInvariantHelper(node.right, node.key, hi);
}
// Return true if there are no keys.
public boolean isEmpty() {
return root == null;
}
// Return the number of keys.
public int size() {
return treeSize;
}
// Return true if the key has an associated value.
public boolean containsKey(K key) {
return get(key) != null;
}
// Look up a key.
public V get(K key) {
return getHelper(root, key);
}
// Recursive helper method for 'get'.
V getHelper(Node node, K key) {
if (node == null)
return null;
if (node.key.compareTo(key) > 0)
return getHelper(node.left, key);
else if (node.key.compareTo(key) < 0)
return getHelper(node.right, key);
else // node.key == key
return node.value;
}
// Add a key-value pair, or update the value associated with an existing key.
// Returns the previous value associated with the key,
// or null if the key wasn't previously present.
public V put(K key, V value) {
root = putHelper(root, key, value);
if (oldValue == null)
treeSize++;
return oldValue;
}
// Recursive helper method for 'put'.
// Stores the previous value in 'oldValue';
Node putHelper(Node node, K key, V value) {
if (node == null) {
oldValue = null;
return new Node(key, value, null, null);
} else if (node.key.compareTo(key) > 0) {
node.left = putHelper(node.left, key, value);
node.updateHeight();
} else if (node.key.compareTo(key) < 0) {
node.right = putHelper(node.right, key, value);
node.updateHeight();
} else { // node.key == key
oldValue = node.value;
node.value = value;
}
return rebalance(node);
}
// Used by put, remove, putHelper and removeHelper,
// in order to return the value previously stored in the node.
private V oldValue;
// Delete a key.
// Returns the previous value associated with the key,
// or null if the key wasn't previously present.
public V remove(K key) {
root = removeHelper(root, key);
if (oldValue != null)
treeSize--;
return oldValue;
}
// Recursive helper method for 'remove'.
Node removeHelper(Node node, K key) {
if (node == null) {
oldValue = null;
return null;
} else if (node.key.compareTo(key) > 0) {
node.left = removeHelper(node.left, key);
node.updateHeight();
return rebalance(node);
} else if (node.key.compareTo(key) < 0) {
node.right = removeHelper(node.right, key);
node.updateHeight();
return rebalance(node);
} else { // node.key == key
if (node.left == null) {
oldValue = node.value;
return node.right;
} else if (node.right == null) {
oldValue = node.value;
return node.left;
} else {
Node predecessor = largestNode(node.left);
oldValue = node.value;
node.key = predecessor.key;
node.value = predecessor.value;
node.left = removeHelper(node.left, predecessor.key);
node.updateHeight();
return rebalance(node);
}
}
}
// Find the largest key.
public K lastKey() {
if (root == null)
return null;
else
return largestNode(root).key;
}
// Helper method for 'lastKey'.
// Returns the node instead, as that's useful in 'removeHelper'.
Node largestNode(Node node) {
// This one is maybe easier to implement non-recursively :)
while (node.right != null)
node = node.right;
return node;
}
// Repair the AVL invariant by rebalancing the node.
Node rebalance(Node node) {
if (node == null) return node;
int diff = node.heightDiff();
if (diff == 2) { // Left-leaning
int leftDiff = node.left.heightDiff();
if (leftDiff == -1) { // Left-right - convert to left-left
node.left = rotateLeft(node.left);
node.updateHeight();
}
return rotateRight(node);
} else if (diff == -2) { // Right-leaning
int rightDiff = node.right.heightDiff();
if (rightDiff == 1) { // Right-left - convert to right-right
node.right = rotateRight(node.right);
node.updateHeight();
}
return rotateLeft(node);
} else
return node;
}
Node rotateLeft(Node node) {
// Left rotation.
//
// x y
// / \ / \
// A y ===> x C
// / \ / \
// B C A B
//
// Variables are named according to the picture above.
Node x = node;
Node A = x.left;
Node y = x.right;
Node B = y.left;
Node C = y.right;
return new Node(y.key, y.value, new Node(x.key, x.value, A, B), C);
}
Node rotateRight(Node node) {
// Right rotation.
//
// x y
// / \ / \
// y C ===> A x
// / \ / \
// A B B C
//
// Variables are named according to the picture above.
Node x = node;
Node y = x.left;
Node A = y.left;
Node B = y.right;
Node C = x.right;
return new Node(y.key, y.value, A, new Node(x.key, x.value, B, C));
}
// Iterate through all keys.
// This is called when the user writes 'for (Key key: bst) { ... }.'
public Iterator<K> iterator() {
// The easiest way to solve this is to add all keys to an
// ArrayList, then iterate through that.
ArrayList<K> keys = new ArrayList<>();
iteratorHelper(root, keys);
return keys.iterator();
}
// Recursive helper method for 'iterator'
void iteratorHelper(Node node, ArrayList<K> keys) {
if (node == null) return;
iteratorHelper(node.left, keys);
keys.add(node.key);
iteratorHelper(node.right, keys);
}
}
# Python does not have internal classes, so we have to make the tree node class standalone.
class Node:
"""A node in an AVL tree."""
def __init__(self, key, value, left = None, right = None):
self.key = key
self.value = value
self.left = left
self.right = right
self.update_height()
def height(self):
"""Return the height of a tree. Also works for None."""
if self is None:
return 0
else:
return self._height
def update_height(self):
"""Recompute the value of the height field.
Must be called every time the height of the tree could change."""
self._height = 1 + max(Node.height(self.left), Node.height(self.right))
def height_diff(self):
"""Return the height difference, left height - right height."""
return Node.height(self.left) - Node.height(self.right)
class AVLMap(Map):
"""A dictionary implemented using a binary search tree."""
def __init__(self):
self.root = None
self.treeSize = 0
def check_invariant(self):
"""Check that the invariant holds."""
size = self.check_invariant_helper(self.root, None, None)
assert size == self.treeSize, "wrong tree size"
@staticmethod
def check_invariant_helper(node, lo, hi):
"""Helper method for 'check_invariant'.
Checks that the node is the root of a valid AVL tree, and that
all keys k satisfy lo < k < hi. The test lo < k is skipped
if lo is None, and k < hi is skipped if hi is None."""
if node is None: return 0
assert lo is None or node.key > lo, "key too small"
assert hi is None or node.key < hi, "key too big"
assert node.height_diff() <= 1, "too left-leaning"
assert node.height_diff() >= -1, "too right-leaning"
# Keys in the left subtree should be < node.key
# Keys in the right subtree should be > node.key
return (1 +
AVLMap.check_invariant_helper(node.left, lo, node.key) +
AVLMap.check_invariant_helper(node.right, node.key, hi))
def isEmpty(self):
"""Return true if there are no keys."""
return self.root is None
def size(self):
"""Return the number of keys."""
return self.treeSize
def containsKey(self, key):
"""Return true if the key has an associated value."""
return self.get(key) is not None
def get(self, key):
"""Look up a key."""
return self.get_helper(self.root, key)
@staticmethod
def get_helper(node, key):
"""Helper method for 'get'."""
if node is None:
return None
elif node.key > key:
return AVLMap.get_helper(node.left, key)
elif node.key < key:
return AVLMap.get_helper(node.right, key)
else:
return node.value
def put(self, key, value):
"""Add a key-value pair, or update the value associated with an existing key.
Returns the value previously associated with the key,
or None if the key was not present."""
self.root, old_value = self.put_helper(self.root, key, value)
if old_value is None:
self.treeSize += 1
return old_value
@staticmethod
def put_helper(node, key, value):
"""Recursive helper method for 'put'.
Returns the updated node, and the value previously associated with the key."""
if node is None:
return Node(key, value, None, None), None
elif node.key > key:
node.left, old_value = AVLMap.put_helper(node.left, key, value)
node.update_height()
elif node.key < key:
node.right, old_value = AVLMap.put_helper(node.right, key, value)
node.update_height()
else: # node.key == key
old_value = node.value
node.value = value
return AVLMap.rebalance(node), old_value
def remove(self, key):
"""Delete a key.
Returns the value previously associated with the key,
or None if the key was not present."""
self.root, old_value = self.remove_helper(self.root, key)
if old_value is not None:
self.treeSize -= 1
return old_value
@staticmethod
def remove_helper(node, key):
"""Helper method for 'remove'.
Returns the updated node, and the value previously associated with the key."""
if node is None:
return None, None
elif node.key > key:
node.left, old_value = AVLMap.remove_helper(node.left, key)
node.update_height()
return AVLMap.rebalance(node), old_value
elif node.key < key:
node.right, old_value = AVLMap.remove_helper(node.right, key)
node.update_height()
return AVLMap.rebalance(node), old_value
else: # node.key == key
if node.left is None:
return node.right, node.value
elif node.right is None:
return node.left, node.value
else:
predecessor = AVLMap.largestNode(node.left)
old_value = node.value
node.key = predecessor.key
node.value = predecessor.value
node.left, _ = AVLMap.remove_helper(node.left, predecessor.key)
node.update_height()
return AVLMap.rebalance(node), old_value
def lastKey(self):
"""Find the largest key."""
if self.root is None:
return None
else:
return self.largestNode(self.root).key
@staticmethod
def largestNode(node):
"""Find the node having the largest key."""
while node.right is not None:
node = node.right
return node
@staticmethod
def rebalance(node):
if node is None: return None
diff = node.height_diff()
if diff == 2: # Left-leaning
left_diff = node.left.height_diff()
if left_diff == -1: # Left-right - convert to left-left
node.left = AVLMap.rotate_left(node.left)
node.update_height()
return AVLMap.rotate_right(node)
elif diff == -2: # Right-leaning
right_diff = node.right.height_diff()
if right_diff == 1: # Right-left - convert to right-right
node.right = AVLMap.rotate_right(node.right)
node.update_height()
return AVLMap.rotate_left(node)
else:
return node
@staticmethod
def rotate_left(node):
"""
Left rotation.
x y
/ \ / \
A y ===> x C
/ \ / \
B C A B
"""
# Variables are named according to the picture above.
x = node
A = x.left
y = x.right
B = y.left
C = y.right
return Node(key = y.key, value = y.value,
left =
Node(key = x.key, value = x.value,
left = A, right = B),
right = C)
@staticmethod
def rotate_right(node):
"""
Right rotation.
x y
/ \ / \
y C ===> A x
/ \ / \
A B B C
"""
# Variables are named according to the picture above.
x = node
y = x.left
A = y.left
B = y.right
C = x.right
return Node(key = y.key, value = y.value,
left = A,
right =
Node(key = x.key, value = x.value,
left = B, right = C))
def __iter__(self):
"""Iterate through all keys.
This is called when the user writes 'for key in bst: ...'."""
return self.iter_helper(self.root)
@staticmethod
def iter_helper(node):
"""Helper method for '__iter__'."""
# This method is a generator:
# https://docs.python.org/3/howto/functional.html#generators
# Generators are an easy way to make iterators
if node is None:
return
else:
for key in AVLMap.iter_helper(node.left):
yield key
yield node.key
for key in AVLMap.iter_helper(node.right):
yield key
def __getitem__(self, key):
"""This is called when the user writes 'x = bst[key]'."""
return self.get(key)
def __setitem__(self, key, value):
"""This is called when the user writes 'bst[key] = value'."""
self.put(key, value)
def __contains__(self, key):
"""This is called when the user writes 'key in bst'."""
return self.containsKey(key)
def __delitem__(self, key):
"""This is called when the user writes 'del bst[key]'."""
self.remove(key)


