8.2.1 Simple Mod Function

Consider the following hash function used to hash integers to a table of sixteen slots.

function hashInt(x):
    return x % 16

Here “%” is the symbol for the [mod] function.

Recall that the values 0 to 15 can be represented with four bits (i.e., 0000 to 1111). The value returned by this hash function depends solely on the least significant four bits of the key. Because these bits are likely to be poorly distributed (as an example, a high percentage of the keys might be even numbers, which means that the low order bit is zero), the result will also be poorly distributed. This example shows that the size of the table $M$ can have a big effect on the performance of a hash system because the table size is typically used as the modulus to ensure that the hash function produces a number in the range 0 to $M-1$.

8.2.2 Binning

Say we are given keys in the range 0 to 999, and have a hash table of size 10. In this case, a possible hash function might simply divide the key value by 100. Thus, all keys in the range 0 to 99 would hash to slot 0, keys 100 to 199 would hash to slot 1, and so on. In other words, this hash function “bins” the first 100 keys to the first slot, the next 100 keys to the second slot, and so on.

Binning in this way has the problem that it will cluster together keys if the distribution does not divide evenly on the high-order bits. In the above example, if more records have keys in the range 900-999 (first digit 9) than have keys in the range 100-199 (first digit 1), more records will hash to slot 9 than to slot 1. Likewise, if we pick too big a value for the key range and the actual key values are all relatively small, then most records will hash to slot 0. A similar, analogous problem arises if we were instead hashing strings based on the first letter in the string.

In general with binning we store the record with key value $i$ at array position $i/X$ for some value $X$ (using integer division). A problem with Binning is that we have to know the key range so that we can figure out what value to use for $X$. Let’s assume that the keys are all in the range 0 to 999. Then we want to divide key values by 100 so that the result is in the range 0 to 9. There is no particular limit on the key range that binning could handle, so long as we know the maximum possible value in advance so that we can figure out what to divide the key value by. Alternatively, we could also take the result of any binning computation and then mod by the table size to be safe. So if we have keys that are bigger than 999 when dividing by 100, we can still make sure that the result is in the range 0 to 9 with a mod by 10 step at the end.

Binning looks at the opposite part of the key value from the mod function. The mod function, for a power of two, looks at the low-order bits, while binning looks at the high-order bits. Or if you want to think in base 10 instead of base 2, modding by 10 or 100 looks at the low-order digits, while binning into an array of size 10 or 100 looks at the high-order digits.

As another example, consider hashing a collection of keys whose values follow a normal distribution, as illustrated by Figure #HashNormal. Keys near the mean of the normal distribution are far more likely to occur than keys near the tails of the distribution. For a given slot, think of where the keys come from within the distribution. Binning would be taking thick slices out of the distribution and assign those slices to hash table slots. If we use a hash table of size 8, we would divide the key range into 8 equal-width slices and assign each slice to a slot in the table. Since a normal distribution is more likely to generate keys from the middle slice, the middle slot of the table is most likely to be used. In contrast, if we use the mod function, then we are assigning to any given slot in the table a series of thin slices in steps of 8. In the normal distribution, some of these slices associated with any given slot are near the tails, and some are near the center. Thus, each table slot is equally likely (roughly) to get a key value.

Figure: Binning vs. modulus

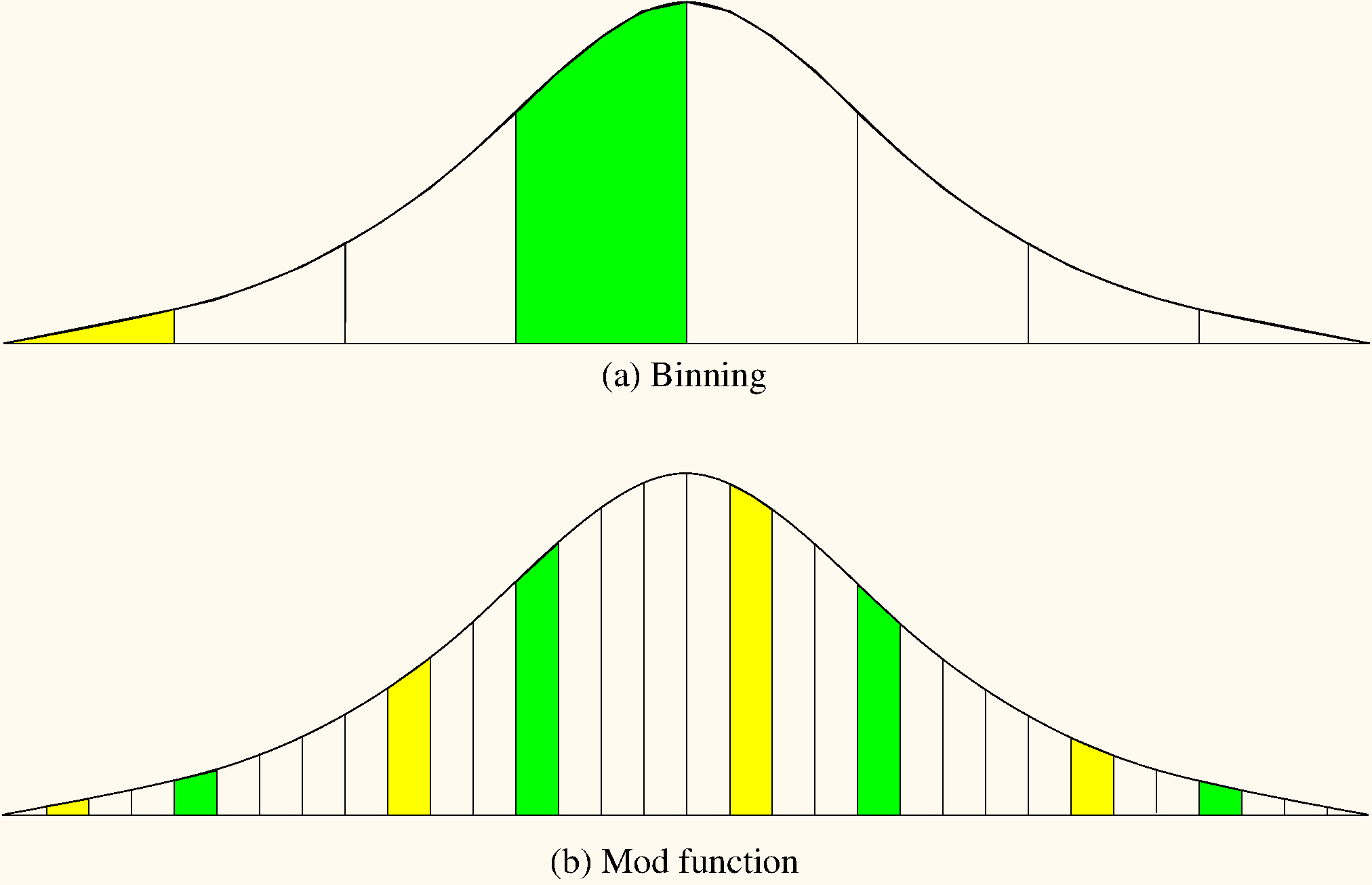
A comparison of binning vs. modulus as a hash function.

8.2.3 The Mid-Square Method

A good hash function to use with integer key values is the mid-square method. The mid-square method squares the key value, and then takes out the middle $r$ bits of the result, giving a value in the range 0 to $2^{r}-1$. This works well because most or all bits of the key value contribute to the result. For example, consider records whose keys are 4-digit numbers in base 10, as shown in Figure #MidSquareFig. The goal is to hash these key values to a table of size 100 (i.e., a range of 0 to 99). This range is equivalent to two digits in base 10. That is, $r = 2$. If the input is the number 4567, squaring yields an 8-digit number, 20857489. The middle two digits of this result are 57. All digits of the original key value (equivalently, all bits when the number is viewed in binary) contribute to the middle two digits of the squared value. Thus, the result is not dominated by the distribution of the bottom digit or the top digit of the original key value. Of course, if the key values all tend to be small numbers, then their squares will only affect the low-order digits of the hash value.

Figure: Mid-square method

An example of the mid-square method. This image shows the traditional gradeschool long multiplication process. The value being squared is 4567. The result of squaring is 20857489. At the bottom, of the image, the value 4567 is show again, with each digit at the bottom of a “V”. The associated “V” is showing the digits from the result that are being affected by each digit of the input. That is, “4” affects the output digits 2, 0, 8, 5, an 7. But it has no affect on the last 3 digits. The key point is that the middle two digits of the result (5 and 7) are affected by every digit of the input.

Here is a little calculator for you to see how this works. Start with ‘4567’ as an example.

8.2.4 A Simple Hash Function for Strings

Now we will examine some hash functions suitable for storing strings of characters. We start with a simple summation function.

function hashString(string, M):
    sum = 0
    for each char in string:
        sum = sum + ord(char)
    return sum % M

This function sums the ASCII values of the letters in a string. If the hash table size $M$ is small compared to the resulting summations, then this hash function should do a good job of distributing strings evenly among the hash table slots, because it gives equal weight to all characters in the string. This is an example of the folding method to designing a hash function.

As with many other hash functions, the final step is to apply the modulus operator to the result, using table size $M$ to generate a value within the table range. If the sum is not sufficiently large, then the modulus operator will yield a poor distribution. For example, because the ASCII value for ‘A’ is 65 and ‘Z’ is 90, sum will always be in the range 650 to 900 for a string of ten upper case letters. For a hash table of size 100 or less, a reasonable distribution results. For a hash table of size 1000, the distribution is terrible because only slots 650 to 900 can possibly be the home slot for some key value, and the values are not evenly distributed even within those slots.

Another problem is that the order of the characters in the string has no effect on the result. E.g., all permutations of the string “ABCDEFG” will result in the same hash value.

Now you can try it out with this calculator.

8.2.5 Improved String Folding

If we instead multiply the hash with a prime number, before adding the next character, we get a much better distribution of the hash codes. This is Java’s default hash code for strings, where the prime number is 31.

function hashStringImproved(string, M):
    sum = 0
    for char in string:
        sum = 31 * sum + ord(char)
    return sum % M

Mathematically, the hash function is $s_0\cdot 31^{n-1} + s_1\cdot 31^{n-2} + ... + s_{n-2}\cdot 31^1 + s_{n-1}\cdot 31^0$. This number grows quite fast when the string gets longer, but that’s not a problem because Java will do an implicit modulo $2^{32}$ on each iteration.

For example, if the string “ABC” is passed to hashStringImproved, the resulting hash value will be $65\cdot 31^2 + 66\cdot 31 + 67 = 64,578$. If the table size is 101 then the modulus function will cause this key to hash to slot 39 in the table.

Now you can try it out with this calculator.

For any sufficiently long string, the sum will typically cause a 32-bit integer to overflow (thus losing some of the high-order bits) because the resulting values are so large. But this causes no problems when the goal is to compute a hash function.

8.2.6 Hash Function Practice

Now here is an exercise to let you practice these various hash functions. You should use the calculators above for the more complicated hash functions.

8.2.7 Practice questions: Hash functions

Here are some review questions.