9.1 Graph Representations
There are two commonly used methods for representing graphs. The adjacency matrix for a graph is a array. We typically label the vertices from through . Row of the adjacency matrix contains entries for Vertex . Column in row is marked if there is an edge from to and is not marked otherwise. The space requirements for the adjacency matrix are .
The second common representation for graphs is the adjacency list. The adjacency list is an array of linked lists. The array is items long, with position storing a pointer to the linked list of edges for Vertex . This linked list represents the edges by the vertices that are adjacent to Vertex .
Here is an example of the two representations on a directed graph. The entry for Vertex 0 stores 1 and 4 because there are two edges in the graph leaving Vertex 0, with one going to Vertex 1 and one going to Vertex 4. The list for Vertex 2 stores an entry for Vertex 4 because there is an edge from Vertex 2 to Vertex 4, but no entry for Vertex 3 because this edge comes into Vertex 2 rather than going out.
Representing a directed graph.
Both the adjacency matrix and the adjacency list can be used to store directed or undirected graphs. Each edge of an undirected graph connecting Vertices and is represented by two directed edges: one from to and one from to . Here is an example of the two representations on an undirected graph. We see that there are twice as many edge entries in both the adjacency matrix and the adjacency list. For example, for the undirected graph, the list for Vertex 2 stores an entry for both Vertex 3 and Vertex 4.
Representing an undirected graph.
The storage requirements for the adjacency list depend on both the number of edges and the number of vertices in the graph. There must be an array entry for each vertex (even if the vertex is not adjacent to any other vertex and thus has no elements on its linked list), and each edge must appear on one of the lists. Thus, the cost is .
Sometimes we want to store weights or distances with each each edge, such as in Figure #GraphTerms (c). This is easy with the adjacency matrix, where we will just store values for the weights in the matrix. In Figure #Directed and Figure #Undirected we store a value of “1” at each position just to show that the edge exists. That could have been done using a single bit, but since bit manipulation is typically complicated in most programming languages, an implementation might store a byte or an integer at each matrix position. For a weighted graph, we would need to store at each position in the matrix enough space to represent the weight, which might typically be an integer.
The adjacency list needs to explicitly store a weight with each edge. In the adjacency list shown below, each linked list node is shown storing two values. The first is the index for the neighbor at the end of the associated edge. The second is the value for the weight. As with the adjacency matrix, this value requires space to represent, typically an integer.
Which graph representation is more space efficient depends on the number of edges in the graph. The adjacency list stores information only for those edges that actually appear in the graph, while the adjacency matrix requires space for each potential edge, whether it exists or not. However, the adjacency matrix requires no overhead for pointers, which can be a substantial cost, especially if the only information stored for an edge is one bit to indicate its existence. As the graph becomes denser, the adjacency matrix becomes relatively more space efficient. Sparse graphs are likely to have their adjacency list representation be more space efficient.
Example: Memory usage
Assume that a vertex index requires two bytes, a pointer requires four bytes, and an edge weight requires two bytes. Then, each link node in the adjacency list needs bytes. The adjacency matrix for the directed graph above requires bytes while the adjacency list requires bytes. For the undirected version of the graph above, the adjacency matrix requires the same space as before, while the adjacency list requires bytes (because there are now 12 edges represented instead of 6).
The adjacency matrix often requires a higher asymptotic cost for an algorithm than would result if the adjacency list were used. The reason is that it is common for a graph algorithm to visit each neighbor of each vertex. Using the adjacency list, only the actual edges connecting a vertex to its neighbors are examined. However, the adjacency matrix must look at each of its potential edges, yielding a total cost of time when the algorithm might otherwise require only time. This is a considerable disadvantage when the graph is sparse, but not when the graph is closer to full.
9.1.1 Practice questions: Graph space requirements
Warning! Read the conditions for the problems in this set very carefully!
Assume for an directed unweighted graph with 6 vertices and 14 edges, that a vertex index requires 2 bytes, and a pointer requires 4 bytes.
Calculate the byte requirements for an adjacency list.
- Since the graph is unweighted, the adjacency list does not store any weight information.
- The adjacency list has an array (of size ) which points to a list of edges.
- Every edge appears once on the list. And for each edge there has to be a vertex ID and a pointer to the next edge.
- It uses bytes.
Assume for an directed unweighted graph with 6 vertices and 14 edges, that a vertex index requires 2 bytes, and a pointer requires 4 bytes.
Calculate the byte requirements for an adjacency matrix.
- Since the graph is unweighted, you can assume that each matrix element stores one byte to represent the edge.
- The matrix is by .
- Each position of the matrix needs one byte.
- It uses bytes.
Assume for an directed weighted graph with 9 vertices and 11 edges, that a vertex index requires 5 bytes, a pointer requires 4 bytes. and that edge weights require 8 bytes.
Calculate the byte requirements for an adjacency list.
- The adjacency list has an array (of size ) which points to a list of edges.
- Every edge appears once on the list. And for each edge there has to be a vertex ID, a weight and a pointer to the next edge.
- It uses bytes.
Assume for an directed weighted graph with 9 vertices and 11 edges, that a vertex index requires 5 bytes, a pointer requires 4 bytes. and that edge weights require 8 bytes.
Calculate the byte requirements for an adjacency matrix.
- The matrix is by .
- Each position of the matrix needs byte.
- It uses bytes.
Assume for an undirected unweighted graph with 7 vertices and 17 edges, that a vertex index requires 6 bytes, and a pointer requires 2 bytes.
Calculate the byte requirements for an adjacency list.
- Since the graph is unweighted, the adjacency list does not store any weight information.
- Since the graph is undirected, each undirected edge is represented by two directed edges.
- The adjacency list has an array (of size ) which points to a list of edges.
- Every edge appears twice on the list (the graph is undirected, so we need the directed edge in each direction). And for each edge there has to be a vertex ID and a pointer to the next edge.
- It uses bytes.
Assume for an undirected unweighted graph with 7 vertices and 17 edges, that a vertex index requires 6 bytes, and a pointer requires 2 bytes.
Calculate the byte requirements for an adjacency matrix.
- Since the graph is unweighted, you can assume that each matrix element stores one byte to represent the edge.
- Since the graph is undirected, each undirected edge is represented by two directed edges.
- The matrix is by .
- Each position of the matrix needs one byte.
- It uses bytes.
Assume for an undirected weighted graph with 10 vertices and 15 edges, that a vertex index requires 1 byte, a pointer requires 2 bytes. and that edge weights require 4 bytes.
Calculate the byte requirements for an adjacency list.
- Since the graph is undirected, each undirected edge is represented by two directed edges.
- The adjacency list has an array (of size ) which points to a list of edges.
- Every edge appears twice on the list (the graph is undirected, so we need the directed edge in each direction). And for each edge there has to be a vertex ID, a weight and a pointer to the next edge.
- It uses bytes.
Assume for an undirected weighted graph with 10 vertices and 15 edges, that a vertex index requires 1 byte, a pointer requires 2 bytes, and that edge weights require 4 bytes.
Calculate the byte requirements for an adjacency matrix.
- Since the graph is undirected, each undirected edge is represented by two directed edges.
- The matrix is by .
- Each position of the matrix needs byte.
- It uses bytes.
9.1.2 Practice questions: Graph terminology
When a vertex is connected by an edge to a vertex , what is the term for their relationship?
- An edge connecting two vertices is incident on these vertices.
- Two vertices connected by an edge are adjacent.
Answer TRUE or FALSE.
Two vertices of a graph are ADJACENT if there is an edge joining them.
- Neighboring vertices are adjacent to one another.
- Two vertices are considered neighbors if there is an edge connecting them.
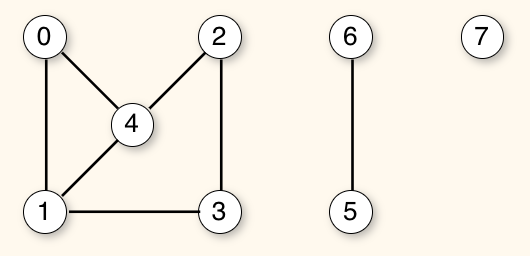
Answer TRUE or FALSE.
Vertices 3 and 4 are adjacent.
- Two vertices are adjacent if there exists and edge between them.

How many connected components does this graph have?
- The maximally connected subgraphs of an undirected graph are called connected components.
- Vertices 0, 1, 2, 3, and 4 form one connnected component
Answer TRUE or FALSE.
A DAG is a directed graph without cycles.
- A DAG is a Directed Acyclic Graph.
- An acyclic graph has no cycles.
Given a subset S of the vertices in a graph, when all vertices in S connect to all other vertices in S, this is called a:
- A clique is a subset of the graph where all the vertices in the subgraph connect to the other vertices.
A complete graph is a clique of size:
- A graph containing all possible edges is said to be a complete graph
- Any subset of where all vertices in the subset connect to all other vertices in the subset is called a clique
- A complete graph is a clique of size .
A graph containing all possible edges is a _____ graph
- A dense graph is a graph with many edges.
- A sparse graph is a graph with relatively few edges.
- A complete graph is a graph containing all possible edges.
A graph without cycles is called a/an:
- An acyclilc graph has no cycles.
The number of edges incident to a vertex called its:
- An edge connecting vertices is said to be incident.
- The degree of a vertex is the number of graph edges it touches.
A digraph is a:
- A directed graph is also called a digraph.
A graph with directed edges is called a
- A graph with edges directed from one vertex to another is a directed graph.
Answer TRUE or FALSE.
All graphs must have edges.
- A graph is a set of edges and vertcies.
- The set of edges may be empty.
A free tree is:
- A free tree is a connected, undirected graph with no cycles.
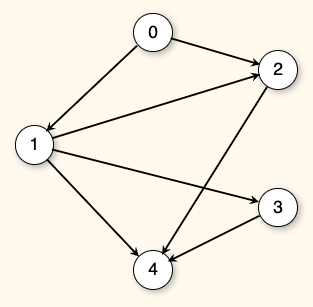
What is the out-degree of Vertex 1?
- The in-degree of a vertex is the number of edges going into the vertex.
- The out-degree of a vertex is the number of edges going out of the vertex.
- Vertex 1 has an three outgoing and two incoming edges.

What is the in-degree of Vertex 2?
- The in-degree of a vertex is the number of edges going into the vertex.
- The out-degree of a vertex is the number of edges going out of the vertex.
- Vertex 2 has an one outgoing and two incoming edges.
Answer TRUE or FALSE.
Two vertices can be adjacent even if they are not neighbors.
- Two vertices are consider neighbors if there is an edge connecting them.
- Neighboring vertices are adjacent to one another.
A simple cycle:
- A cyle is simple if all vertices on the cycle are distinct, with the first and last vertices being the same.
A simple path:
- A path is simple if all vertices on the path are distinct.
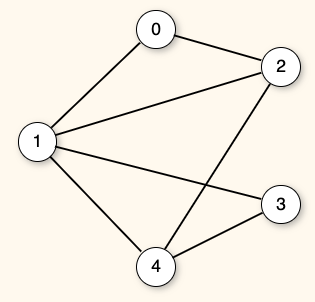
What is the degree of Vertex 4?
- The degree of a vertex is the number of edges that the vertex touches.
- Vertex 4 has three incident edges.
Answer TRUE or FALSE.
A weighted graph must have edge weights and be directed.
- A weighted graph must have edge weights.
- A weighted graph can be a directed or undirected graph.