DSABook – Review questions

13.11 Review questions

This final section contains some review questions about the contents of this chapter.

13.11.1 Review questions: Graph terminology

When a vertex $Q$ is connected by an edge to a vertex $K$ , what is the term for their relationship?

$Q$ and $K$ are adjacent
$Q$ and $K$ are incident
$Q$ and $K$ are insecure
$Q$ and $K$ are isolated

An edge connecting two vertices is incident on these vertices.
Two vertices connected by an edge are adjacent.

Answer TRUE or FALSE.

Two vertices of a graph are ADJACENT if there is an edge joining them.

True
False

Neighboring vertices are adjacent to one another.
Two vertices are considered neighbours if there is an edge connecting them.

Answer TRUE or FALSE.

Vertices 3 and 4 are adjacent.

True
False

Two vertices are adjacent if there exists and edge between them.

How many connected components does this graph have?

The maximally connected subgraphs of an undirected graph are called connected components.
Vertices 0, 1, 2, 3, and 4 form one connnected component

Answer TRUE or FALSE.

A DAG is a directed graph without cycles.

True
False

A DAG is a Directed Acyclic Graph.
An acyclic graph has no cycles.

Given a subset S of the vertices in a graph, when all vertices in S connect to all other vertices in S, this is called a:

A clique is a subset of the graph where all the vertices in the subgraph connect to the other vertices.

A complete graph is a clique of size:

$|V|$
$|E|$
$|n|$
$n$

A graph containing all possible edges is said to be a complete graph
Any subset of $V$ where all vertices in the subset connect to all other vertices in the subset is called a clique
A complete graph is a clique of size $|V|$ .

A graph containing all possible edges is a _____ graph

A dense graph is a graph with many edges.
A sparse graph is a graph with relatively few edges.
A complete graph is a graph containing all possible edges.

A graph without cycles is called a/an:

An acyclilc graph has no cycles.

The number of edges incident to a vertex called its:

An edge connecting vertices is said to be incident.
The degree of a vertex is the number of graph edges it touches.

A digraph is a:

directed graph
undirected graph
connected component
DAG

A directed graph is also called a digraph.

A graph with directed edges is called a

directed graph
labeled graph
weighted graph
complete graph

A graph with edges directed from one vertex to another is a directed graph.

Answer TRUE or FALSE.

All graphs must have edges.

False
True

A graph is a set of edges and vertcies.
The set of edges may be empty.

A free tree is:

a connected graph with no cycles
a connected graph with only simple cycles
an unconnected graph with no cycles

A free tree is a connected, undirected graph with no cycles.

What is the out-degree of vertex 1?

The in-degree of a vertex is the number of edges going into the vertex.
The out-degree of a vertex is the number of edges going out of the vertex.
Vertex 1 has an three outgoing and two incoming edges.

What is the in-degree of vertex 2?

The in-degree of a vertex is the number of edges going into the vertex.
The out-degree of a vertex is the number of edges going out of the vertex.
Vertex 2 has an one outgoing and two incoming edges.

Answer TRUE or FALSE.

Two vertices can be adjacent even if they are not neighbours.

False
True

Two vertices are consider neighbours if there is an edge connecting them.
Neighboring vertices are adjacent to one another.

A simple cycle:

must have all vertices unique except that the first and last vertices are the same
allows repetition of vertices so long as the length of the path is less than 5
allows repetition of vertices so long as no edge is repeated
must have all vertices be unique

A cyle is simple if all vertices on the cycle are distinct, with the first and last vertices being the same.

A simple path:

must have all vertices be unique
allows repetition of vertices so long as the length of the path is less than 5
allows repetition of vertices so long as no edge is repeated
must have all vertices unique except that the first and last vertices are the same

A path is simple if all vertices on the path are distinct.

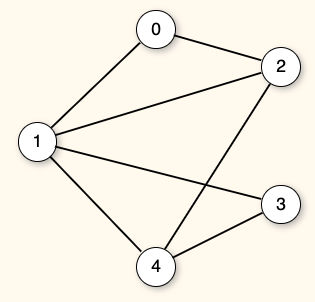
What is the degree of vertex 4?

The degree of a vertex is the number of edges that the vertex touches.
Vertex 4 has three incident edges.

Answer TRUE or FALSE.

A weighted graph must have edge weights and be directed.

False
True

A weighted graph must have edge weights.
A weighted graph can be a directed or undirected graph.

13.11.2 Review questions: Graph space requirements

Warning! Read the conditions for the problems in this set very carefully!

Assume for an directed unweighted graph with 6 vertices and 14 edges, that a vertex index requires 2 bytes, and a pointer requires 4 bytes.

Calculate the byte requirements for an adjacency list.

Since the graph is unweighted, the adjacency list does not store any weight information.
The adjacency list has an array (of size $|V|$ ) which points to a list of edges.
Every edge appears once on the list. And for each edge there has to be a vertex ID and a pointer to the next edge.
It uses $(|V| \cdot \textrm{pointer}) + (|E| \cdot (\textrm{vertex-index} + \textrm{pointer}))$ bytes.

Assume for an directed unweighted graph with 6 vertices and 14 edges, that a vertex index requires 2 bytes, and a pointer requires 4 bytes.

Calculate the byte requirements for an adjacency matrix.

Since the graph is unweighted, you can assume that each matrix element stores one byte to represent the edge.
The matrix is $|V|$ by $|V|$ .
Each position of the matrix needs one byte.
It uses $|V|^2 \cdot 1$ bytes.

Assume for an directed weighted graph with 9 vertices and 11 edges, that a vertex index requires 5 bytes, a pointer requires 4 bytes. and that edge weights require 8 bytes.

Calculate the byte requirements for an adjacency list.

The adjacency list has an array (of size $|V|$ ) which points to a list of edges.
Every edge appears once on the list. And for each edge there has to be a vertex ID, a weight and a pointer to the next edge.
It uses $(|V| \cdot \textrm{pointer}) + (|E| \cdot (\textrm{vertex-index} + \textrm{edge-weight} + \textrm{pointer}))$ bytes.

Assume for an directed weighted graph with 9 vertices and 11 edges, that a vertex index requires 5 bytes, a pointer requires 4 bytes. and that edge weights require 8 bytes.

Calculate the byte requirements for an adjacency matrix.

The matrix is $|V|$ by $|V|$ .
Each position of the matrix needs $\textrm{edge-weight}$ byte.
It uses $|V|^2 \cdot \textrm{edge-weight}$ bytes.

Assume for an undirected unweighted graph with 7 vertices and 17 edges, that a vertex index requires 6 bytes, and a pointer requires 2 bytes.

Calculate the byte requirements for an adjacency list.

Since the graph is unweighted, the adjacency list does not store any weight information.
Since the graph is undirected, each undirected edge is represented by two directed edges.
The adjacency list has an array (of size $|V|$ ) which points to a list of edges.
Every edge appears twice on the list (the graph is undirected, so we need the directed edge in each direction). And for each edge there has to be a vertex ID and a pointer to the next edge.
It uses $(|V| \cdot \textrm{pointer}) + (2 \cdots |E| \cdot (\textrm{vertex-index} + \textrm{pointer}))$ bytes.

Assume for an undirected unweighted graph with 7 vertices and 17 edges, that a vertex index requires 6 bytes, and a pointer requires 2 bytes.

Calculate the byte requirements for an adjacency matrix.

Since the graph is unweighted, you can assume that each matrix element stores one byte to represent the edge.
Since the graph is undirected, each undirected edge is represented by two directed edges.
The matrix is $|V|$ by $|V|$ .
Each position of the matrix needs one byte.
It uses $|V|^2 \cdot 1$ bytes.

Assume for an undirected weighted graph with 10 vertices and 15 edges, that a vertex index requires 1 byte, a pointer requires 2 bytes. and that edge weights require 4 bytes.

Calculate the byte requirements for an adjacency list.

Since the graph is undirected, each undirected edge is represented by two directed edges.
The adjacency list has an array (of size $|V|$ ) which points to a list of edges.
Every edge appears twice on the list (the graph is undirected, so we need the directed edge in each direction). And for each edge there has to be a vertex ID, a weight and a pointer to the next edge.
It uses $(|V| \cdot \textrm{pointer}) + (2 \cdots |E| \cdot (\textrm{vertex-index} + \textrm{edge-weight} + \textrm{pointer}))$ bytes.

Assume for an undirected weighted graph with 10 vertices and 15 edges, that a vertex index requires 1 byte, a pointer requires 2 bytes, and that edge weights require 4 bytes.

Calculate the byte requirements for an adjacency matrix.

Since the graph is undirected, each undirected edge is represented by two directed edges.
The matrix is $|V|$ by $|V|$ .
Each position of the matrix needs $\textrm{edge-weight}$ byte.
It uses $|V|^2 \cdot \textrm{edge-weight}$ bytes.

13.11.3 Summary questions

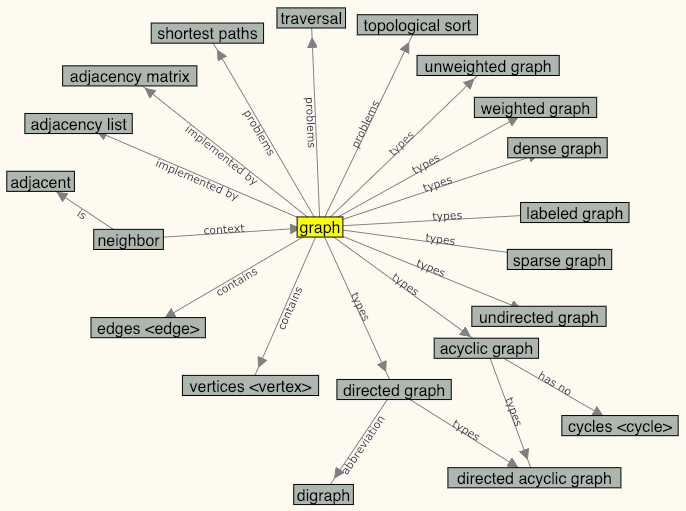
Answer TRUE or FALSE.

An acyclic graph can have cycles.

True
False

Look at these terms on the concept map.

A Graph data structure contains ______

Vertices and edges
Adjacency lists and Adjacency matrices
Directed and undirected graphs
Weighed and unweighted graphs

Look at these terms on the concept map.

Another name for “Directed graph” is ______

Digraph
Direct graph
Bigraph
Dir-graph

Look at these terms on the concept map.

Which of the following is true?

None of the above
A graph may contain no edges and many vertices
A graph may contain many edges and no vertices
A graph may contain no edges and no vertices
None of the above

Look at these terms on the concept map.

A Graph data structure can be implemented by ______

Look at these terms on the concept map.

A directed graph that has no cycles is a(n) _____

Acyclic directed graph
Directed graph
Undirected graph
Acyclic graph

Look at these terms on the concept map.

Which of these terms does not fit with the others?

Dense graph
Shortest path
Traversal
Topological sort

Look at these terms on the concept map.

Which of the following are a type of graph data structure?

Look at these terms on the concept map.