5.1 Definitions and Properties
A binary tree is made up of a finite set of elements called nodes. This set either is empty or consists of a node called the root together with two binary trees, called the left and right subtrees, which are disjoint from each other and from the root. (Disjoint means that they have no nodes in common.) The roots of these subtrees are children of the root. There is an edge from a node to each of its children, and a node is said to be the parent of its children.
If is a sequence of nodes in the tree such that is the parent of for , then this sequence is called a path from to . The length of the path is . If there is a path from node to node , then is an ancestor of , and is a descendant of . Thus, all nodes in the tree are descendants of the root of the tree, while the root is the ancestor of all nodes. The depth of a node in the tree is the length of the path from the root of the tree to . The height of a tree is the depth of the deepest node in the tree. All nodes of depth are at level in the tree. The root is the only node at level 0, and its depth is 0. A leaf node is any node that has two empty children. An internal node is any node that has at least one non-empty child.
A binary tree. Node is the root. Nodes and are ’s children. Nodes and together form a subtree. Node has two children: Its left child is the empty tree and its right child is . Nodes , , and are ancestors of . Nodes , , and make up level 2 of the tree; node is at level 0. The edges from to to to form a path of length 3. Nodes , , , and are leaves. Nodes , , , , and are internal nodes. The depth of is 3. The height of this tree is 3.
Two different binary trees. (a) A binary tree whose root has a non-empty left child. (b) A binary tree whose root has a non-empty right child. (c) The binary tree of (a) with the missing right child made explicit. (d) The binary tree of (b) with the missing left child made explicit.
Figure #BinExample illustrates the various terms used to identify parts of a binary tree. Figure #BinDiff illustrates an important point regarding the structure of binary trees. Because all binary tree nodes have two children (one or both of which might be empty), the two binary trees of Figure #BinDiff are not the same.
Two restricted forms of binary tree are sufficiently important to warrant special names. Each node in a full binary tree is either (1) an internal node with exactly two non-empty children or (2) a leaf. A complete binary tree has a restricted shape obtained by starting at the root and filling the tree by levels from left to right. In the complete binary tree of height , all levels except possibly level are completely full. The bottom level has its nodes filled in from the left side.
Examples of full and complete binary trees.
Figure #FullComplete illustrates the differences between full and complete binary trees. There is no particular relationship between these two tree shapes; that is, the tree (a) is full but not complete while the tree (b) is complete but not full. The heap data structure is an example of a complete binary tree. The Huffman coding tree is an example of a full binary tree.
Note: While these definitions for full and complete binary tree are the ones most commonly used, they are not universal. Because the common meaning of the words “full” and “complete” are quite similar, there is little that you can do to distinguish between them other than to memorize the definitions. Here is a memory aid that you might find useful: “Complete” is a wider word than “full”, and complete binary trees tend to be wider than full binary trees because each level of a complete binary tree is as wide as possible.
5.1.1 Practice questions: Binary tree definition
Which statement is false?
- Look carefully at the definition for a binary tree.
- It states that every binary tree is either empty, or it has a root node and two binary trees as children.
- So, every binary tree node has two children, but not every binary tree has a node.
What is the minimum number of nodes in a complete binary tree with height 3?
- Start filling in the tree level by level.
- Stop when you draw the first node at level 3.
Select the one true statement.
- Not every binary tree is either complete or full.
- Not every complete binary tree is full.
- Not every full binary tree is complete.
- Some complete trees are full.
What is the minimum number of nodes in a full binary tree with height 3?
- First, draw a vertical chain of 4 nodes. This is a tree with height 3.
- Next, add nodes to make the tree be full.
Suppose T is a binary tree with 14 nodes. What is the minimum possible height of T?
- Try drawing this as a complete treee.
- That is, build a tree of 14 nodes by filling it in level by level.
What is the minimum number of internal nodes in a binary tree with 8 nodes?
- Try drawing some trees. Your best bet is to try and make it full.
5.1.2 Binary tree exercises
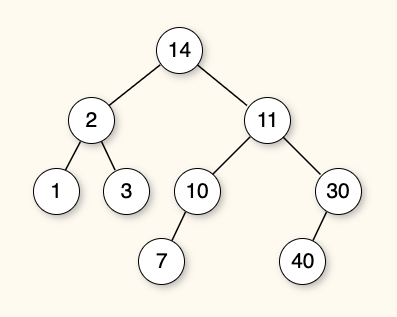
How many internal nodes does this tree have?
- Anything that is not a leaf node is an internal node. Internal nodes might have 1 or 2 children.
What is the height of this tree?
- Count the number of steps to the deepest node.
How many leaf nodes does this tree have?
- Anything that has no children is a leaf node.
How many nodes in the tree have at least one sibling?
- Siblings must have the same parent. If a node has two children, then each such child has a sibling.
How many descendents does the root of this tree have?
- Every node except the root is a descendent.
What is the depth of this tree?
- Nodes have depth.
Which statement is correct?
- Do any internal nodes have only one child? If so, the tree is not full.
- A complete tree fills in nodes level by level, with the bottom level filled in from left to right.